Statistik und Datenanalyse: Aufbau

Mittelwert, Standardabweichung, Korrelation

Benjamin Fretwurst
PDF-Version der Folien

Inhalt

• 1 Modulintro
  • 1.1 Lernziele des Moduls
  • 1.2 Leistungsnachweis
  • 1.3 Inhalt und Aufwandt
  • 1.4 Material
• 2 Befragung
• 3 Was bisher geschah
  • 3.1 Univariate Statistik
  • 3.2 Bivariate Statistik
  • 3.3 Hypothesentesten
• LEF 1
  • Essayfragen
  • MC-Fragen
• Take Home
• Ausblick

1 Modulintro

Lernziele heute

Modulorga

• Lernziele und Inhalte von «Statistik: Aufbau»
• Orga
• Lernmaterialien

Anschluss an Statistik: Einführung

• Mittelwert
• Streuung
• Inferenz
  • Punktschätzung (Standardfehler)
  • Intervallschätzung
  • Tests
• Kovarianz und Korrelation

1.1 Lernziele des Moduls

Grundlagenkenntnisse

• Sie erlangen Kenntnisse multivariater Statistik.
• Verständnis empirischer Forschungsbeiträge
• Umgang mit Vorlagen für die Anwendung der Verfahren in R.

Praktische Statistik für «Methoden Aufbau»

Sie können Analysemethoden anwenden, die Sie für Ihr Projekt in Methoden Aufbau brauchen.

Verständnis fortgeschrittener Statistik für die Forschungsseminare

Vorbereitung auf die Forschungsseminare, in denen Sie weiterführende Analyseverfahren verstehen müssen (Texte und Analysen) und teilweise auch anwenden.

1.1.1 Voraussetzungen

Inhaltliche Voraussetzungen

• Deskriptive und induktive Statistik aus «Statistik und Datenanalyse: Einführung»

• heute Rückblick

• Folien der Statistik-Einführungs-Vorlesung (+ Buch Ihrer Wahl)

Technische Voraussetzung

• R

• R-Studio (oder VS-Code)

• Weiteres siehe Anleitung R-Installationsanleitung

1.2 Leistungsnachweis

Was ist Prüfungsstoff?

• Folien
• Vorlesung
• Begleittext

Prüfungstermin (Major + Minor)

• Hauptklausur
  • 03.01.2024
  • 14:30–15:30 (60 Minuten)
  • BYOD ➪ [Y-15-G-60 + Y24-G-45]
• Wiederholungsklausur Major und Minor
  • 07.02.2024
  • 14:30–15:30 (60 Minuten)
  • BYOD ➪ Y-15-G-60

1.3 Inhalt und Aufwandt

Inhalte

1. Uni- und Bivariate Statistik
2. GLM – Regression
3. GLM – BLUE
4. Übung: GLM I
   
5. GLM – Kategoriale UV
6. GLM – Interaktionen
7. GLM – Übung II

8. Dimensionsreduktion
9. Übung: Dimensionsreduktion
10. LogReg und ML
11. Übung: Machine Learning
12. Clusteranalyse
13. Übung: R
14. Zusammenfassung

Aufwandt für 6 ECTS

Aufwand	in h	h/Woche	Punkte
Besuch der Vorlesung	21	1.5	0.7
Vor und Nachbereitung	21	1.5	0.7
Lesen der Texte	42	3.0	1.4
Übungsaufgaben in R	50	3.6	1.7
Prüfungsvorbereitung	42	3.0	1.4
Studienteilnahmepunkte	4	0.3	0.1
Summe für 6 ECTS * 30h	180	12.9	6.0

1.4 Material

E-Learning – OLAT

OLAT

• Mitteilungen
• Forum
  • Diskussionen und Fragen
  • Klausurvorbereitung
• Studienteilnahmepunkte 🔗

R-Seite und Begleittext (BETA!)

R-Seite

Auf r.ikmz.uzh.ch/Wissen_macht_R! finden Sie Anleitungen zur Installation von R und R-Studio sowie Beispielskripte und Vorlagen, die wir vor allem auch für brauchen, bzw. Ihnen helfen sollen.

Begleittext ist noch BETA!

Der Begleittext auf stat.ikmz.uzh.ch/Aufbau wird während des Semesters deutlich überarbeitet und ist daher BETA! Es gibt keine vollständige Gewähr für Fehlerfreiheit!

Zusatzliteratur (Wiederholung Statistik Einführung)

Für die Wiederholung von «Statistik: Einführung».

2 Befragung

Erwartungen

R-Code anzeigen

DATEN   |>
    haven::zap_formats() |>
  kreuz_skala(Varlist = c(E201_01, E201_02, E201_10, E201_11), Labelweite = 20, Loeschen = "Erwartungen STAT A") 

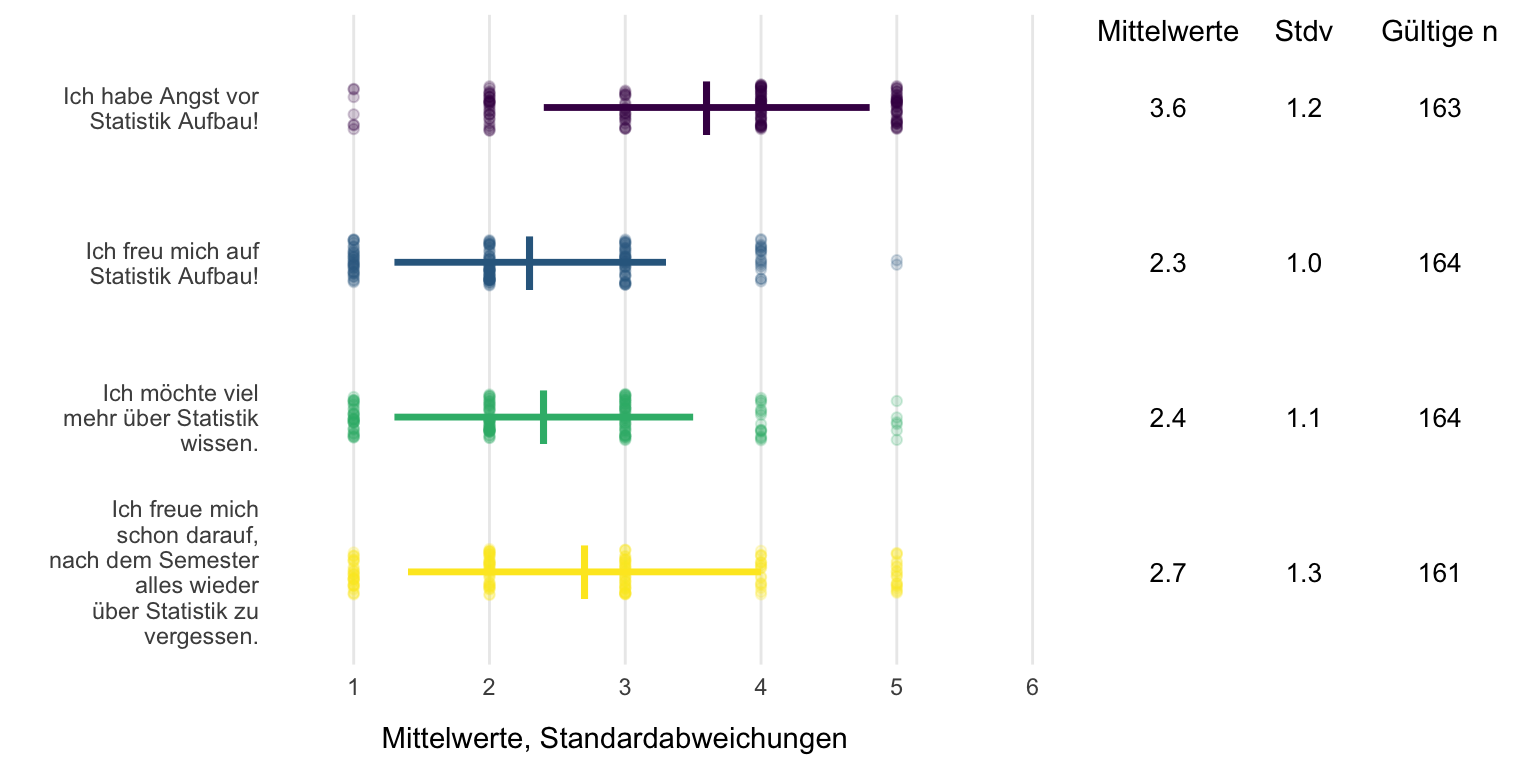
Umgang mit R

R-Code anzeigen

DATEN  |>
  kreuz_skala(Varlist = c(E201_07, E201_06),  Labelweite = 30, Loeschen = "Erwartungen STAT A") 

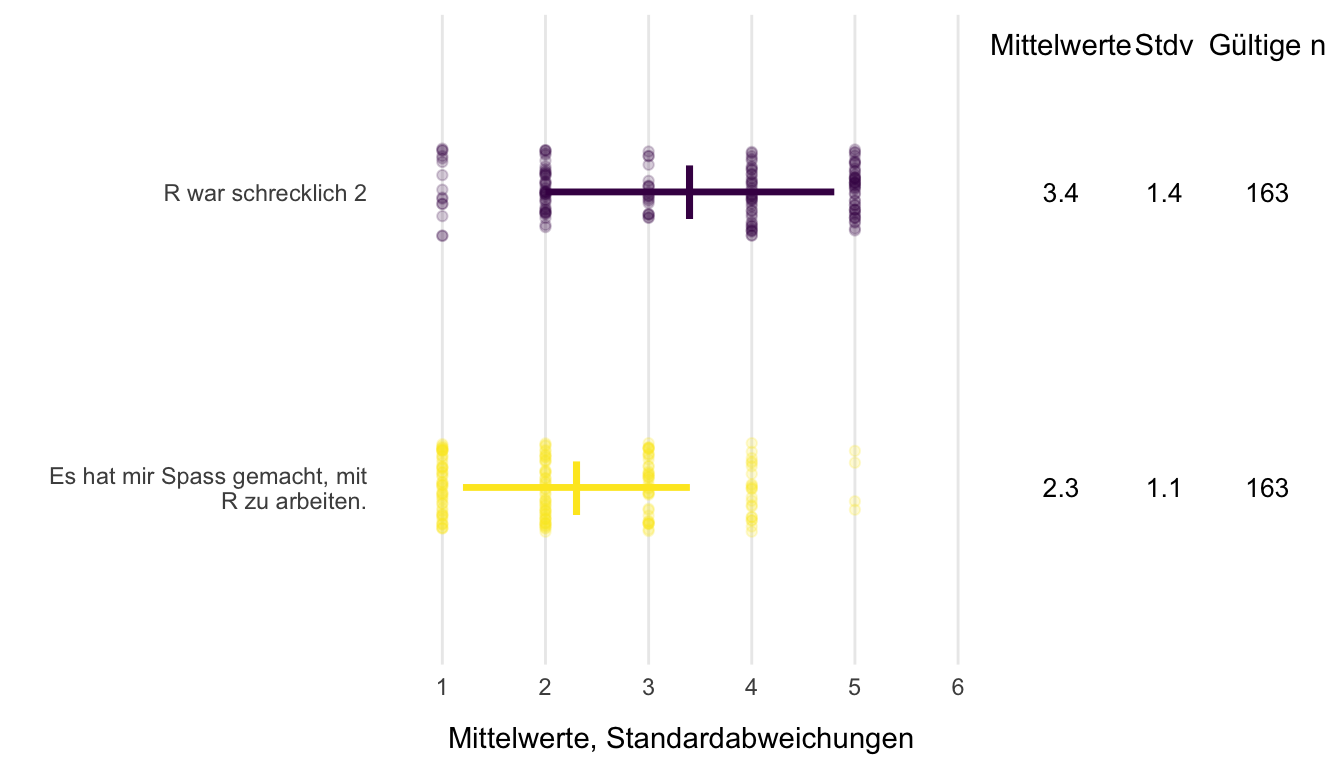
Ziele

R-Code anzeigen

DATEN |>
    haven::zap_formats()  |>
  kreuz_skala(Varlist = c( E201_08, E201_09, E201_11),  Labelweite = 30, Loeschen = "Erwartungen STAT A") 

Was geht mit Formeln?

R-Code anzeigen

DATEN |>
    haven::zap_formats() |>
  haven::zap_formats()  |>
  kreuz_skala(Varlist = c(E201_13, E201_12),  Labelweite = 30, Loeschen = "Erwartungen STAT A") 

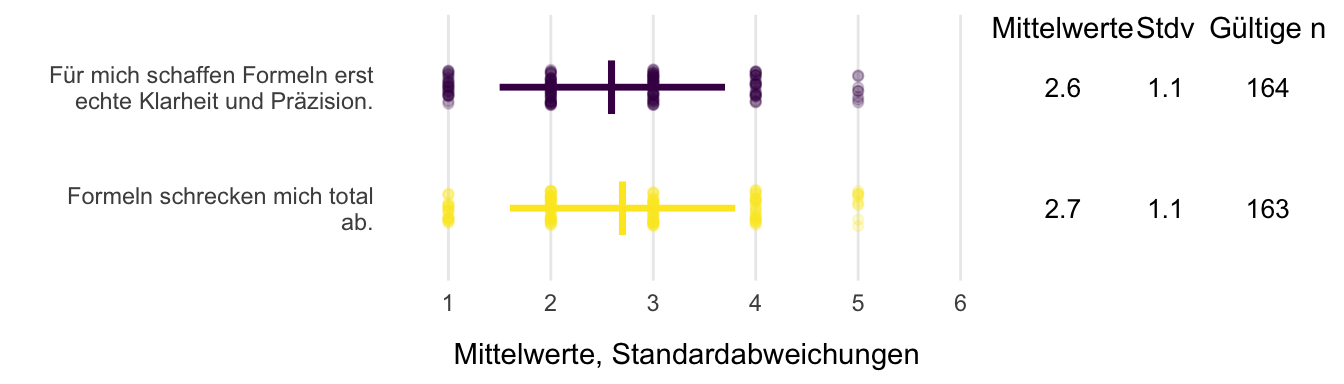
Spass und Freude

R-Code anzeigen

 DATEN |>
    haven::zap_formats() |>
    select(E201_02, E201_06) |> 
  filter(E201_02 >= 0 & E201_06 >= 0) |> # sjmisc::frq()
#    sjlabelled::label_to_colnames() |> 
    ggplot(aes(x = E201_06, y = E201_02)) +
    geom_jitter(width = 0, height = 0) + 
  labs(x = "Es hat mir Spass gemacht, mit R zu arbeiten", y = "Ich freu mich auf Statistik Aufbau")+
  geom_smooth(method=lm) +
    theme_minimal()

Statistik war leicht

R-Code anzeigen

 DATEN |>
    haven::zap_formats()  |>
    select(E201_02, E201_06) |> # sjmisc::frq()
    filter(E201_02 >= 0 & E201_06 >= 0) |> 
    sjlabelled::remove_all_labels() |> 
    ggplot(aes(x = E201_06, y = E201_02,  colour = E201_06)) +
    geom_jitter(width = 0.2, height = .2) + 
  scale_color_viridis() +
  labs(x = "Es hat mir Spass gemacht, mit R zu arbeiten.", y = "Ich freu mich auf Statistik Aufbau!")+
  geom_smooth(method=lm) +
  ggpubr::stat_cor(method = "pearson", label.x = 4, label.y = 1.3, p.digits = 3, p.accuracy = .05) +
    theme_minimal() + 
  theme(legend.position = "none")

Statistik war leicht (doppelt)

R-Code anzeigen

 DATEN |>
    haven::zap_formats() |>
    select(E102_01, E201_03) |> # sjmisc::frq()
    filter(E102_01 >= 0 & E201_03 >= 0) |> 
    sjlabelled::remove_all_labels() |> 
      ggplot(aes(x = E102_01, y = E201_03, colour = E102_01)) +
    geom_jitter(width = 0.2, height = 0.2) + 
  scale_color_viridis() +
  labs(x = "Statistik war leicht", y = "Statistik war leicht 2")+
  geom_smooth(method=lm) +
  ggpubr::stat_cor(method = "pearson", label.x = 4, label.y = 1.3, p.digits = 3, p.accuracy = .05) +
    theme_minimal() + 
  theme(legend.position = "none")

Korrelationen

R-Code anzeigen

DATEN |>
    haven::zap_formats() |> 
  select(E102_01:E102_06) |> 
  sjlabelled::label_to_colnames() |> 
  cor() |> 
  ggcorrplot::ggcorrplot(hc.order = TRUE, type = "lower",
   lab = TRUE)
  

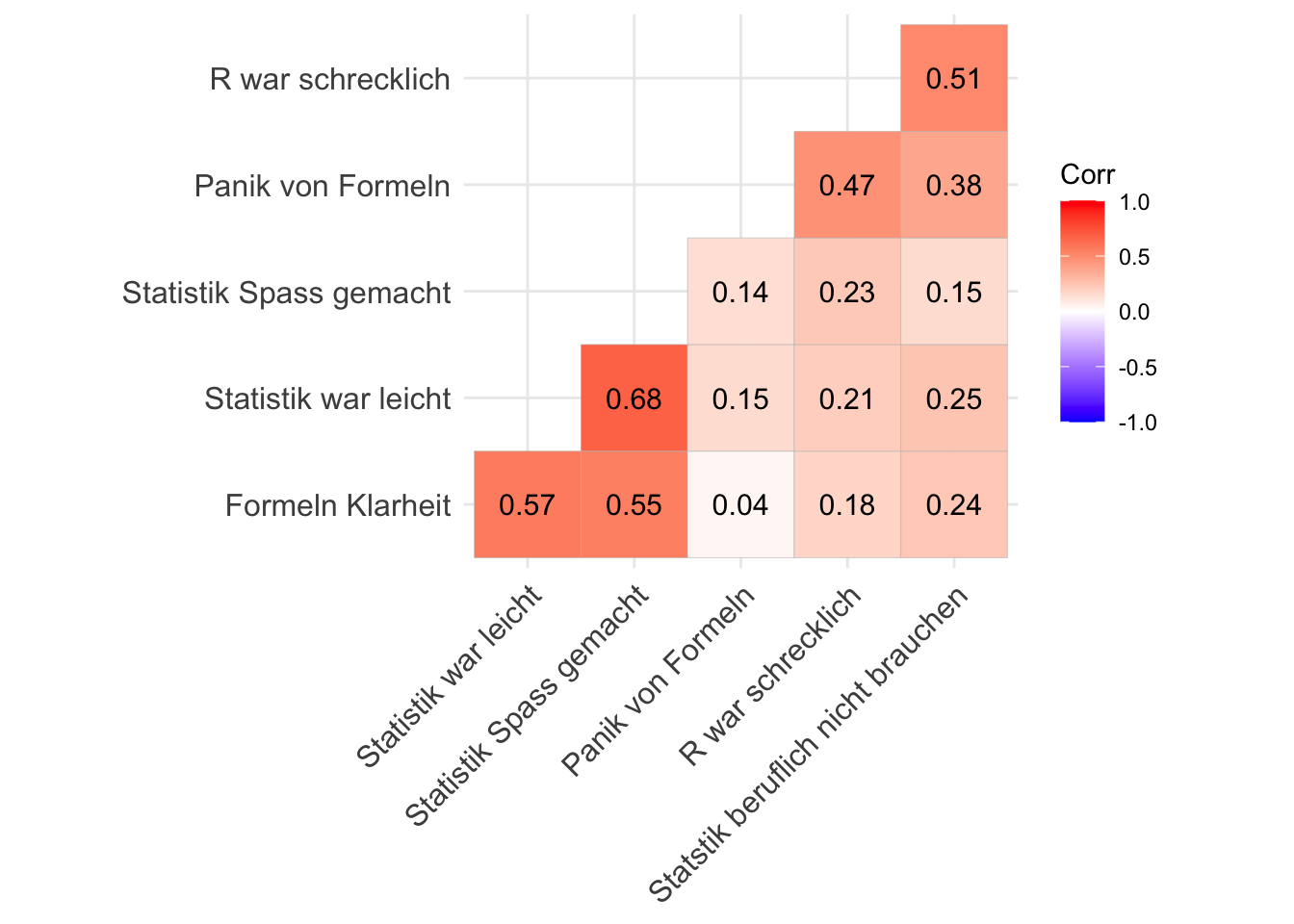
Korrelation doppelte Frage

R-Code anzeigen

DATEN |>
    haven::zap_formats() |> 
  select(E102_01:E102_06, E201_03, E201_07) |> 
  sjlabelled::label_to_colnames() |> 
  cor() |> 
  ggcorrplot::ggcorrplot(hc.order = TRUE, type = "lower",
   lab = TRUE)

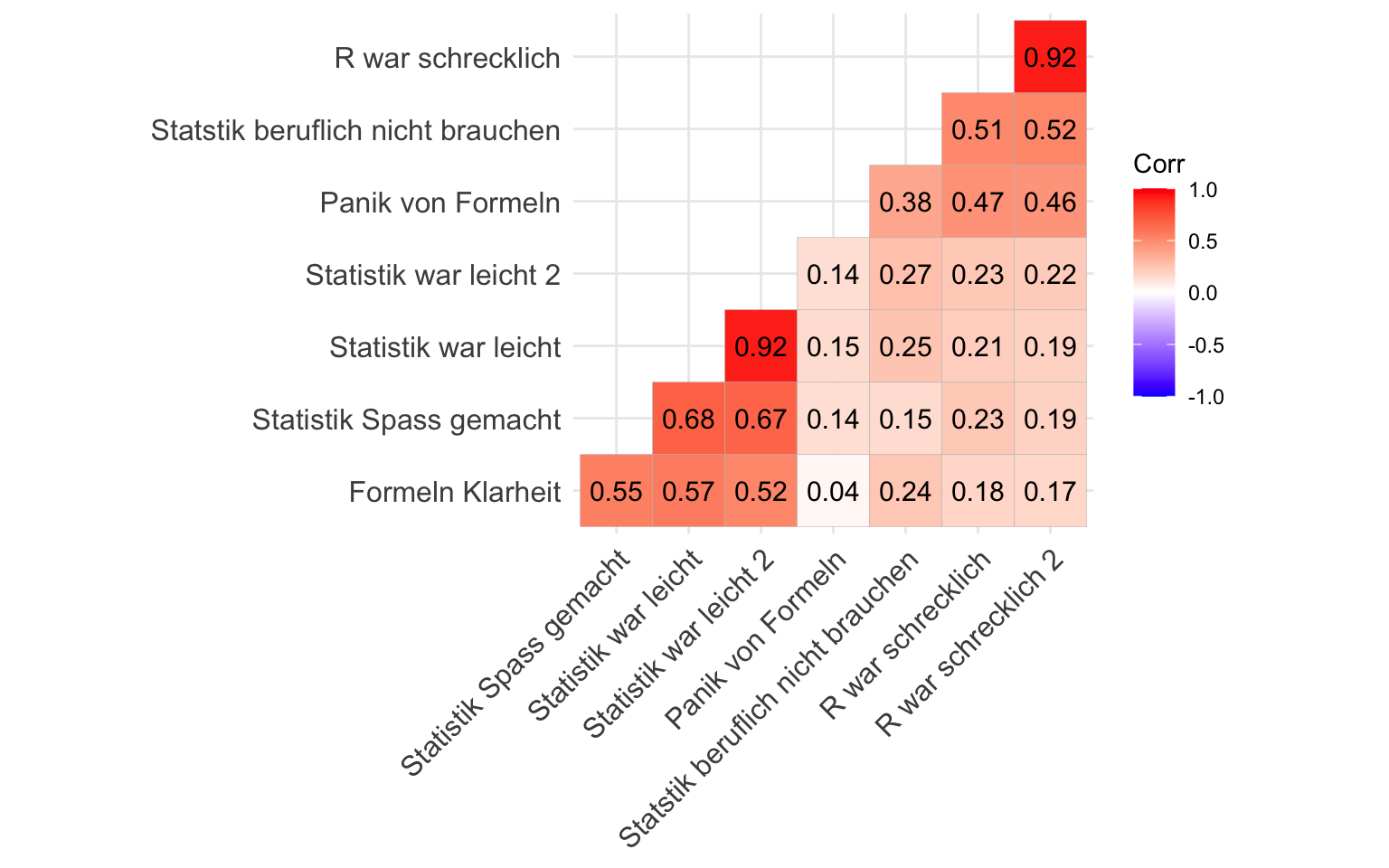
3 Was bisher geschah

3.1 Univariate Statistik

3.1.1 Mittelwert

Der Mittelwert ist das Gleiche wie ein Durchschnitt.

\begin{aligned} \overline{x} = & \frac{1}{n}\sum_i^n(x_i)\\ \overline{y} = & \frac{1}{n}\sum_i^n(y_i) \end{aligned}

Mittelwert wird geschrieben als Kennwert \overline{x} und Parameter \mu.

3.1.2 Varianz

Die Varianz ist er Mittelwert (Durchschnitt) der quadrierten Abweichungen vom Mittelwert.

\begin{aligned} \sigma^2 = V = & \frac{1}{n} \sum_i^n(x_i-\mu)^2\\ \end{aligned}

Die Varianz als unbekannter Parameter wird als \sigma^2 gekennzeichnet.

3.1.3 Standardabweichung

Die Standardabweichung ist die Wurzel der Varianz. Gefühlt ist die Standardabweichung sowas wie die durchschnittliche Abweichung (Beträge) vom Mittelwert (eben durch die Quadrierung und Rückrechnung über die Wurzel nicht ganz dasselbe).

\begin{aligned} s_x = \hat{\sigma}_x = & \sqrt{\frac{1}{n-1} \sum_i^n(x_i-\overline{x})^2} \end{aligned}

Die Standardabweichung als unbekannter Parameter wird als \sigma_x gekennzeichnet und der Kennwert als s_x.

Standardabweichung im Vergleich

Standardfehler

Definition und Eigenschaften

Die Standardabweichung einer Stichprobenkennwerte-Verteilung nennt man Standardfehler (standard error, SE). Wenn es sich um eine Verteilung von Mittelwerten handelt Standardfehler des Mittelwerts (s_{\overline{x}}).

Der Standardfehler gibt an, wie gut \overline{x} den Populationsparameter \mu schätzt.

Eigenschaften

• Der Standardfehler jedes Kennwertes nimmt mit grösser werdendem n ab 👉 \sigma_{\overline{x}} ist umgekehrt proportional zu \sqrt{n}.

• Je stärker das gemessene Merkmal in der Population streut, desto grösser der Standardfehler 👉 \sigma_{\overline{x}} ist proportional zu \sigma.

Die Formel:

\begin{aligned} \sigma_{\overline{x}}&=\sqrt{\frac{\sigma^2}{n}}\\ &=\frac{\sigma}{\sqrt{n}} \end{aligned}

Effekte des Stichprobenumfangs

Standardisierung

Standardisierung

Standardisierung von Verteilungen und Kennwerten macht alles vergleichbar.

• z_i=\frac{x_i-\overline{x}}{s}.
• Eine z-Verteilte Grösse hat immer: \overline{x}=0 und s = 1.
• Standardisierte Verteilungen und Kennwerte sind vergleichbar.

Konfidenzintervalle für Mittelwerte

Konfidenzintervalle

Konfidenzintervalle geben einen Wertebereich an, in dem die Parameter (GG) der Stichprobenkennwerte mit einer angebbaren Wahrscheinlichkeit liegen.

\begin{aligned} \text{KI: } \overline{X}\pm z_1 \cdot SE\\ \text{KI: } \overline{X}\pm z_1 \cdot \frac{s_x}{\sqrt{n}}\\ \text{KI}_{l.05} = \overline{x} - 1.96 \cdot \frac{s_x}{\sqrt{n}}\\ \text{KI}_{r.05} = \overline{x} + 1.96 \cdot \frac{s_x}{\sqrt{n}} \end{aligned}

3.2 Bivariate Statistik

3.2.1 Kovarianz und Korrelation

\begin{aligned} cov = C = & \frac{1}{n}\sum_i^n(x_i-\overline{x}) (y_i-\overline{y})\\[1em] r = & \frac{\sum_i^n(x_i-\overline{x}) (y_i-\overline{y})}{n \cdot s_x \cdot s_y} \end{aligned}

3.3 Hypothesentesten

Testen gegen die Nullhypothese

1. Könnte in der Auswahlgesamtheit der wahre Wert auch 0 sein, oder ein anderes Vorzeichen haben?

2. Die Nullhypothese ist eine statistische Hypothese gegen Falschentscheidungen aufgrund von Zufallsziehungen.

3. Nullhypothesen werden anhand von bekannten Verteilungen getestet.

LEF 1

Essayfragen

1. Was ist der Unterschied zwischen unstandardisierten und standardisierten Kennwerten?

2. Welche Masse der zentralen Tendenz kennen Sie?

3. Welche Streumasse kennen Sie?

4. Was kommt raus, wenn man die Covarianz einer Variablen mit sich selbst berechnet?

5. 1. Welche Skalenniveaus kennen Sie?

   2. Was macht eine Nominalskala aus?

   3. Was macht eine metrische Skala aus?

MC-Fragen

MC 1.1.

MC 1.1: Sind folgende Aussagen richtig oder falsch?

MC_1_1 = [
    ["Der Mittelwert ist dasselbe wie der Durchschnitt.", "richtig"],
    ["Der Mittelwert einer dichotomen Variablen entspricht dem Prozentsatz der 1-Werte.", "richtig"],
    ['Der Mittelwert wird auch als "Mittel" oder "Arithmetisches Mittel" bezeichnet.', "richtig"],
    ["Je grösser ein Mittelwert ist, desto eher ist er signifikant.", "falsch"]
]

viewof answers_1_1 = quizInput({
  questions: MC_1_1,
  options: ["richtig", "falsch"]
})

Punkte_1_1 = {
const Sum = 
    (answers_1_1[0] == MC_1_1[0][1])*1 + 
    (answers_1_1[1] == MC_1_1[1][1])*1 + 
    (answers_1_1[2] == MC_1_1[2][1])*1 + 
    (answers_1_1[3] == MC_1_1[3][1])*1 

var Punkte_1_1 = Sum - 2
if (Punkte_1_1 < 1) {Punkte_1_1 = 0}
return(Punkte_1_1)
}

Punkte:

MC 1.2.

MC 1.2: Sind folgende Aussagen richtig oder falsch?

MC_1_2 = [
    ["Die Standardabweichung ist die standardisierte Form der Varianz.", "falsch"],
    ["Die Standardabweichung hat n-1 Freiheitsgrade.", "richtig"],
    ['Die Standardabweichung "s" liegt immer zwischen 0 und 1.', "falsch"],
    ["Die Standardabweichung ist die durchschnittliche Abweichung vom Mittelwert.", "falsch"]
]

viewof answers_1_2 = quizInput({
  questions: MC_1_2,
  options: ["richtig", "falsch"]
})

Punkte_1_2 = {
const Sum = 
    (answers_1_2[0] == MC_1_2[0][1])*1 + 
    (answers_1_2[1] == MC_1_2[1][1])*1 + 
    (answers_1_2[2] == MC_1_2[2][1])*1 + 
    (answers_1_2[3] == MC_1_2[3][1])*1 

var Punkte_1_2 = Sum - 2
if (Punkte_1_2 < 1) {Punkte_1_2 = 0}
return(Punkte_1_2)
}

Punkte:

MC 1.3.

MC 1.3: Sind folgende Aussagen richtig oder falsch?

MC_1_3 = [
    ["Die Covarianz ist das Quadrat der Korrelation.", "falsch"],
    ["Die Covarianz ist skalenabhängig und kann daher negativ oder positiv und unendlich klein oder gross sein.", "richtig"],
    ['Die Korrelation "r" liegt immer zwischen 0 und 1.', "falsch"],
    ["Eine Korrelation von genau 0 kann nie signifikant sein.", "richtig"]
]

viewof answers_1_3 = quizInput({
  questions: MC_1_3,
  options: ["richtig", "falsch"]
})

Punkte_1_3 = {
const Sum = 
    (answers_1_3[0] == MC_1_3[0][1])*1 + 
    (answers_1_3[1] == MC_1_3[1][1])*1 + 
    (answers_1_3[2] == MC_1_3[2][1])*1 + 
    (answers_1_3[3] == MC_1_3[3][1])*1 

var Punkte_1_3 = Sum - 2
if (Punkte_1_3 < 1) {Punkte_1_3 = 0}
return(Punkte_1_3)
}

Punkte:

MC 1.4.

MC 1.4: Sind folgende Aussagen richtig oder falsch?

MC_1_4 = [
    ["Bei der bivariaten Korrelation sind r und die Wurzel aus $$R^2$$ identisch.", "richtig"],
    ["Das b einer bivariaten Regressionsgeraden liegt immer zwischen -1 und 1.", "falsch"],
    ['Wenn das b nicht signifikant ist, kann nicht mit 95% Wahrscheinlichkeit ausgeschlossen werden, dass es in Wirklichkeit Null ist oder ein zum Stichprobenwert entgegengesetztes Vorzeichen hat.', "richtig"],
    ["Wenn ein b signifikant ist, dann ist auch BETA signifikant.", "richtig"]
]

viewof answers_1_4 = quizInput({
  questions: MC_1_4,
  options: ["richtig", "falsch"]
})

Punkte_1_4 = {
const Sum = 
    (answers_1_4[0] == MC_1_4[0][1])*1 + 
    (answers_1_4[1] == MC_1_4[1][1])*1 + 
    (answers_1_4[2] == MC_1_4[2][1])*1 + 
    (answers_1_4[3] == MC_1_4[3][1])*1 

var Punkte_1_4 = Sum - 2
if (Punkte_1_4 < 1) {Punkte_1_4 = 0}
return(Punkte_1_4)
}

Punkte:

MC 1.5.

MC 1.5: Sind folgende Aussagen richtig oder falsch?

MC_1_5 = [
    ["Statistische Signifikanz bedeutet im Grunde wissenschaftliche Relevanz.", "falsch"],
    ["Bei kleinen Stichproben können Ergebnisse auch schon mal signifikant werden, obwohl die Effekte so kleine sind, dass sie zu vernachlässigen sind.", "falsch"],
    ['Je grösser n, desto schneller wird derselbe Effekt (z.B. Mittelwertunterschied) signifikant.', "richtig"],
    ["Wenn man einmal ein Signifkanzniveau (z.B. 95%) festgelegt hat, sollte man auch dabei bleiben.", "richtig"]
]

viewof answers_1_5 = quizInput({
  questions: MC_1_5,
  options: ["richtig", "falsch"]
})

Punkte_1_5 = {
const Sum = 
    (answers_1_5[0] == MC_1_5[0][1])*1 + 
    (answers_1_5[1] == MC_1_5[1][1])*1 + 
    (answers_1_5[2] == MC_1_5[2][1])*1 + 
    (answers_1_5[3] == MC_1_5[3][1])*1 

var Punkte_1_5 = Sum - 2
if (Punkte_1_5 < 1) {Punkte_1_5 = 0}
return(Punkte_1_5)
}

Punkte:

MC 1.6.

MC 1.6: Sind folgende Aussagen richtig oder falsch?

MC_1_6 = [
    ["Wenn das Konfidenzintervall eines Kennwertes kleiner als .05 ist, dann ist es signifikant.", "falsch"],
    ["Wenn das Konfidenzintervall eines Mittelwertes die 0 nicht einschliesst, dann ist der Mittelwert signifikant von 0 verschieden.", "richtig"],
    ['Wählt man ein höheres Signifikanzniveau (z.B. 99% statt 95%), dann wird das Konfidenzintervall breiter.', "richtig"],
    ["Je breiter ein Konfidenzintervall, desto besser ist ein Kennwert interpretierbar.", "falsch"]
]

viewof answers_1_6 = quizInput({
  questions: MC_1_6,
  options: ["richtig", "falsch"]
})

Punkte_1_6 = {
const Sum = 
    (answers_1_6[0] == MC_1_6[0][1])*1 + 
    (answers_1_6[1] == MC_1_6[1][1])*1 + 
    (answers_1_6[2] == MC_1_6[2][1])*1 + 
    (answers_1_6[3] == MC_1_6[3][1])*1 

var Punkte_1_6 = Sum - 2
if (Punkte_1_6 < 1) {Punkte_1_6 = 0}
return(Punkte_1_6)
}

Punkte:

Punktemax_1 = 12

Punkte_1_Gesamt = Punkte_1_1 + Punkte_1_2 + Punkte_1_3 + Punkte_1_4 + Punkte_1_5 + Punkte_1_6

Prozent_1 = round(100*Punkte_1_Gesamt/Punktemax_1, 0)

Note_1 = round((round(Punkte_1_Gesamt/Punktemax_1,1)*10+2)/2, 1)

Insgesamt von Punkten, was % und etwa einer entspricht.

round = (n, places) => {
  if (!places) return Math.round(n);
  const d = 10 ** places;
  return Math.round(n * d) / d;
}

function quizInput({ questions, options}) {
  let answers = questions.map(() => null);
  let root = htl.html`<div
      style="
        display: grid;
        grid-template-columns: 10% 10% 70% 10%;"
    >
      ${options.map(
        (opt) => htl.html`<div style="font-weight: bold; font-size: HUGE">${opt}</div>`
      )}
      <div style="font-weight: bold">Aussagen</div>
      <div style="font-weight: bold"></div>
      ${Array.from(questions.entries(), ([i, [question, correct]]) =>
        quizInputRow({
          question,
          options,
          correct,
          onChange: (newAnswer) => {
            answers[i] = newAnswer;
            root.value = answers;
            root.dispatchEvent(new CustomEvent("input"));
          }
        })
      )}
    </div>`;
  root.value = answers;
  return root;
}

function quizInputRow({
  question,
  options,
  correct,
  onChange = () => {}
}) {
  let root = htl.html`<div>`;

  function setAnswer(answer, initial = false) {
    morph(
      root,
      htl.html`<div style="display: contents"> 
      <form style="display: contents">
        ${options.map(
          (opt) =>
            htl.html`<label>&emsp;</label> 
            <input  
              name=${question} &emsp;
              type="radio"
              value="${opt}"
              checked=${opt === answer}
              onChange=${() => setAnswer(opt)}
            >
            </input>`
        )}
      </form>
      <div>${question}</div>
      <div> &emsp; ${
       answer === null ? "" : answer === correct ? "💚" : "❌"
      }</div>
    </div>`
    );

    root.value = answer;
    if (!initial) {
      root.dispatchEvent(new CustomEvent("input"));
      onChange(answer);
    }
  }

  setAnswer(null, true);
  return root;
}

morph = require("https://bundle.run/nanomorph@5.4.2")

Take Home

Statistik

• ist ein Modell von Realität
• ist eine mächtige Denkweise
• ist Basis und Kern von Data Science

Aus Statistik Einführung muss sitzen

• Mittelwerte
• Varianz/ Standardabweichung s- Covarianz/ Korrelation

Ausblick

Grundlagen der Modellbildung

Regression mit zwei Unabhängigen

Inferenzstatistische Grundlagen

Punktschätzung, Intervallschätzung, Wahrscheinlichkeitsverteilungen

Grundannahmen von OLS-Schätzungen

mässige Multikollniearität, Homoskedastizität, Modellspezifikation, Linearität