# Prüfe, ob es in dem Ordner in der die Uebung_1_ab.qmd gespeichert ist, einen Unterordner "files" gibt und, wenn nicht, dann lege ihn an.
if(dir.exists("files")){} else {dir.create("files")}
## NULL
# Lade die Installations.R herunter und speichere sie im Unterordner des Projekts unter "files"
download.file("https://stat.ikmz.uzh.ch/Aufbau/Folien/Sitzung_04/files/Installation.R",paste("files/Installation.R") )Statistik und Datenanalyse: Aufbau
Übung 1 – 4. Sitzung
PDF-Version der Folien
Orga
Orga
- Es gibt neue Studienteilnahmestudien!
Lernziele
Grundprinzipien der Regression
- Sinn und Zweck von Quarto
- Einübung Regressionsanalyse
- Übung zur Berechnung von b_2, um zu verstehen, wie die Zusammenhänge bivariat angelegt sind und die übrigen Dritteinflüsse “herausgerechnet” werden
- Vor- und Nachteile der visuellen Residualanalyse vs. Tests
Übung 1 a+b
Ü1.1 Erstellen Sie eine Quarto-Datei.qmd
- Öffnen Sie R-Studio
- In R-Studio ➪ File ➪ New File ➪ Quarto Document…
- Klicken Sie unten links auf «Create Empty Document»
- (Wählen Sie als
title«Erste Regression») - Fügen Sie einen r-Chunk hinzu mit diesem Schalter:
![]()
- speichern Sie an einem günstigen Ort
(am besten in der Cloud + nicht auf Desktop)
Ü1.2 Installation und Setup
Die R-Befehle für die Installation von Paketen haben wir in die Datei “Installation.R” ausgelagert, weil man sie im Grunde jeweils nur einmal braucht. Ich habe Ihnen hier eine Installationsdatei gebaut, mit der Sie die Pakete mit höhrer Erfolgschance installieren können. Mit folgendem Befehl wird diese Datei automatisch von unserer Homepage heruntergeladen und im Unterordner “files” des Projekts gespeichert. Sie können Sie dann dort öffnen und (am besten Zeilenweise) ausführen, wenn Sie die Pakete noch nicht installiert haben.
Für generelle Grundeinstellungen haben wir eine “_common.R” angelegt, in der wir den Aufruf der Basispakete des tidyverse geschrieben haben und andere Optionen und Einstellungen für Designs (wie Farben). Die Datei kann man dann immer am Anfang seiner Quarto-Dateien aufrufen und braucht diese Generaleinstellungen nicht immer wieder neu kopieren. Das ist doch praktisch.
# Prüfe, ob es in dem Ordner in der die Uebung_1_ab.qmd gespeichert ist, einen Unterordner "files" gibt und, wenn nicht, dann lege ihn an.
if(dir.exists("files")){} else {dir.create("files")}
## NULL
download.file("https://stat.ikmz.uzh.ch/Aufbau/Folien/Sitzung_04/files/_common.R", destfile= "files/_common.R")
source("files/_common.R")Ü1.3 Laden Sie die Daten
Laden Sie den Fragebogen hier runter und schauen ihn an.
Laden Sie die Daten und lassen Sie mal die Variablenlabel raus:
R-Code anzeigen
# Wenn wir die Dateien einmal geladen und aufbereitet haben (mit der Extradatei "Aufbereitung.qmd"), dann ist es besser, nicht immer wieder neu die Rohdaten zu laden, sondern die Aufbereiteten.
# Prüfe, ob es in dem Ordner in der die Uebung_1_ab.qmd gespeichert ist, einen Unterordner "files" gibt und, wenn nicht, dann lege ihn an.
if(dir.exists("data")){} else {dir.create("data")}
## NULL
download.file("https://stat.ikmz.uzh.ch/Aufbau/Folien/Sitzung_04/data/Stat_Aufbau_Befragung.RDS", "data/Stat_Aufbau_Befragung.RDS")
DATEN <- readRDS("data/Stat_Aufbau_Befragung.RDS") |>
haven::zap_formats()
# DATEN |> sjlabelled::get_label()
DATEN |>
saveRDS("data/Stat_Aufbau_Befragung.RDS")Ü1.4 Rechnen Sie ein Regressionsmodell
DATEN <- DATEN |> haven::zap_formats()
Modell_1 <- lm(E201_10 ~ E102_02, data = DATEN)
summary(Modell_1)
##
## Call:
## lm(formula = E201_10 ~ E102_02, data = DATEN)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.2726 -0.7684 -0.2641 0.7274 2.7274
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.28105 0.16912 7.575 2.60e-12 ***
## E102_02 0.49578 0.06668 7.435 5.73e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9151 on 162 degrees of freedom
## (3 observations deleted due to missingness)
## Multiple R-squared: 0.2544, Adjusted R-squared: 0.2498
## F-statistic: 55.28 on 1 and 162 DF, p-value: 5.729e-12Was sehen Sie?
- Wie gross ist R^2?
- Wie gross ist die bivariate Korrelation r? (selbst ausrechnen)
- Ist der Zusammenhang positiv oder negativ?
- Ist der Zusammenhang signifikant?
Ü1.5 Verändern Sie das Regressionsmodell
Kopieren Sie den r-Chunk der letzten Folie und setzen Sie andere Variablen ein: Nehmen Sie die Variablen für «Statistik Einführung hat mir viel Spass gemacht» und erklären Sie damit: «Ich freu mich auf Statistik Aufbau!».
Beantworten wieder die Fragen:
- Wie gross ist R^2?
- Wie gross ist die bivariate Korrelation r? (selbst ausrechnen)
- Ist der Zusammenhang positiv oder negativ?
- Ist der Zusammenhang signifikant?
Code
DATEN |> sjmisc::frq(E201_02, E102_02) |>
haven::zap_formats()
## Erwartungen STAT A: Ich freu mich auf Statistik Aufbau! (E201_02) <integer>
## # total N=167 valid N=166 mean=2.31 sd=0.99
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -----------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## -2 | keine Antwort | 0 | 0.00 | 0.00 | 0.00
## -1 | weiss nicht | 0 | 0.00 | 0.00 | 0.00
## 1 | trifft überhaupt nicht zu | 38 | 22.75 | 22.89 | 22.89
## 2 | 2 | 61 | 36.53 | 36.75 | 59.64
## 3 | 3 | 46 | 27.54 | 27.71 | 87.35
## 4 | 4 | 19 | 11.38 | 11.45 | 98.80
## 5 | trifft voll und ganz zu | 2 | 1.20 | 1.20 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## Statistik Spass gemacht (E102_02) <integer>
## # total N=167 valid N=164 mean=2.30 sd=1.07
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## -2 | keine Antwort | 0 | 0.00 | 0.00 | 0.00
## -1 | weiss nicht | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 44 | 26.35 | 26.83 | 26.83
## 2 | 2 | 55 | 32.93 | 33.54 | 60.37
## 3 | 3 | 42 | 25.15 | 25.61 | 85.98
## 4 | 4 | 18 | 10.78 | 10.98 | 96.95
## 5 | 5 trifft voll und ganz zu | 5 | 2.99 | 3.05 | 100.00
## <NA> | <NA> | 3 | 1.80 | <NA> | <NA>
Modell_2 <- lm(E201_02 ~ E102_02, data = DATEN)
summary(Modell_2)
##
## Call:
## lm(formula = E201_02 ~ E102_02, data = DATEN)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.7779 -0.4288 -0.1033 0.5475 1.8967
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.75420 0.12578 5.996 0.0000000127 ***
## E102_02 0.67457 0.04959 13.602 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6806 on 162 degrees of freedom
## (3 observations deleted due to missingness)
## Multiple R-squared: 0.5332, Adjusted R-squared: 0.5303
## F-statistic: 185 on 1 and 162 DF, p-value: < 2.2e-16
# R² = .5332
Modell_2_beta <- lm.beta::lm.beta(Modell_2)
summary(Modell_2_beta)
##
## Call:
## lm(formula = E201_02 ~ E102_02, data = DATEN)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.7779 -0.4288 -0.1033 0.5475 1.8967
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 0.75420 NA 0.12578 5.996 0.0000000127 ***
## E102_02 0.67457 0.73019 0.04959 13.602 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6806 on 162 degrees of freedom
## (3 observations deleted due to missingness)
## Multiple R-squared: 0.5332, Adjusted R-squared: 0.5303
## F-statistic: 185 on 1 and 162 DF, p-value: < 2.2e-16
# r = .73Ü1.6 b_2 aus Korrelationen und SDs berechnen
Note
Lassen Sie die Korrelationen durchlaufen, schauen Sie sich an, wo was steht und setzen Sie es in die Formel für b_2 = \frac{r_{Y2}-r_{23}r_{Y3}}{(1-R_{2.3}^2)}\frac{s_Y}{s_2}, um es zu berechnen.
Also: b_2 = \frac{.50-(-.32\cdot -.23)}{(1-.32^2)}\frac{1.05}{1.07}
R-Code anzeigen
DATEN |>
select(E201_10, E102_02, E102_04) |>
# sjlabelled::label_to_colnames() |>
apaTables::apa.cor.table()
##
##
## Means, standard deviations, and correlations with confidence intervals
##
##
## Variable M SD 1 2
## 1. E201_10 2.42 1.05
##
## 2. E102_02 2.30 1.07 .50**
## [.38, .61]
##
## 3. E102_04 3.64 1.24 -.23** -.32**
## [-.37, -.08] [-.45, -.17]
##
##
## Note. M and SD are used to represent mean and standard deviation, respectively.
## Values in square brackets indicate the 95% confidence interval.
## The confidence interval is a plausible range of population correlations
## that could have caused the sample correlation (Cumming, 2014).
## * indicates p < .05. ** indicates p < .01.
##
beta_2 = (.68 - (.23 * .25)) / ((1-.23^2))
b2 = beta_2 * 1.37/1.42
b2
## [1] 0.6341263Man kann natürlich auch R nutzen
R-Code anzeigen
# Damit es ganz genau wird, filtere ich erstmal alle Fälle raus, die in einer der Variablen ein NA haben:
DATEN_UE1_6 <- DATEN |>
filter(!is.na(E201_10) & !is.na(E102_02) & !is.na(E102_04))
# Mit dem neuen Teildatensatz berechne ich die Korrelationen
r_2y = cor(DATEN_UE1_6$E201_10, DATEN_UE1_6$E102_02)
r_23 = cor(DATEN_UE1_6$E102_02, DATEN_UE1_6$E102_04)
r_3y = cor(DATEN_UE1_6$E201_10, DATEN_UE1_6$E102_04)
# R² ist das Quadrat von r_23
RSQ_23 = r_23^2
# Jetzt noch die Standardfehler von Y und X2
sd_y = sd(DATEN_UE1_6$E201_10, na.rm = TRUE)
sd_x = sd(DATEN_UE1_6$E102_02, na.rm = TRUE)
b2 = (r_2y - r_23 * r_3y) / (1-RSQ_23) * sd_y / sd_x
round(b2, 5)
## [1] 0.4721Ü1.7 Berechnen Sie b_2 mit Hilfe einer Regressionsanalyse
Modell1 <- lm(E201_10 ~ E102_02 + E102_04, data = DATEN)
Modell_1_beta <- lm.beta::lm.beta(Modell1)
summary(Modell_1_beta, digits = digits, maxsum = maxsum)
##
## Call:
## lm(formula = E201_10 ~ E102_02 + E102_04, data = DATEN)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.3852 -0.7194 -0.2281 0.5642 2.7439
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 1.57016 NA 0.32129 4.887 2.46e-06 ***
## E102_02 0.47210 0.48031 0.07031 6.714 3.08e-10 ***
## E102_04 -0.06458 -0.07570 0.06102 -1.058 0.292
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9148 on 161 degrees of freedom
## (3 observations deleted due to missingness)
## Multiple R-squared: 0.2596, Adjusted R-squared: 0.2504
## F-statistic: 28.22 on 2 and 161 DF, p-value: 3.114e-11Ü1.8 Geben Sie mit folgendem Befehl die Tolerance und VIF-Werte raus
olsrr::ols_regress(Modell1)
## Model Summary
## --------------------------------------------------------------
## R 0.509 RMSE 0.915
## R-Squared 0.260 Coef. Var 37.790
## Adj. R-Squared 0.250 MSE 0.837
## Pred R-Squared 0.235 MAE 0.736
## --------------------------------------------------------------
## RMSE: Root Mean Square Error
## MSE: Mean Square Error
## MAE: Mean Absolute Error
##
## ANOVA
## --------------------------------------------------------------------
## Sum of
## Squares DF Mean Square F Sig.
## --------------------------------------------------------------------
## Regression 47.235 2 23.617 28.221 0.0000
## Residual 134.735 161 0.837
## Total 181.970 163
## --------------------------------------------------------------------
##
## Parameter Estimates
## ---------------------------------------------------------------------------------------
## model Beta Std. Error Std. Beta t Sig lower upper
## ---------------------------------------------------------------------------------------
## (Intercept) 1.570 0.321 4.887 0.000 0.936 2.205
## E102_02 0.472 0.070 0.480 6.714 0.000 0.333 0.611
## E102_04 -0.065 0.061 -0.076 -1.058 0.292 -0.185 0.056
## ---------------------------------------------------------------------------------------
olsrr::ols_vif_tol(Modell1)
## Variables Tolerance VIF
## 1 E102_02 0.8987008 1.112717
## 2 E102_04 0.8987008 1.112717Ü1.9 Schauen Sie sich die Residualplotts an

Plot der Residuen
Ü1.10 Testen Sie auf Homoskedastizität
R-Code anzeigen
# Führe einen Breusch-Pagan-Test aus
olsrr::ols_test_breusch_pagan(Modell1)
##
## Breusch Pagan Test for Heteroskedasticity
## -----------------------------------------
## Ho: the variance is constant
## Ha: the variance is not constant
##
## Data
## -----------------------------------
## Response : E201_10
## Variables: fitted values of E201_10
##
## Test Summary
## ----------------------------
## DF = 1
## Chi2 = 2.305095
## Prob > Chi2 = 0.1289504Was sagt Ihnen das?
Ü1.11 Gucken Sie sich den N-Q-Q-Plot an

Normal-Q-Q-Plot
Ü1.12 Und das Histogramm
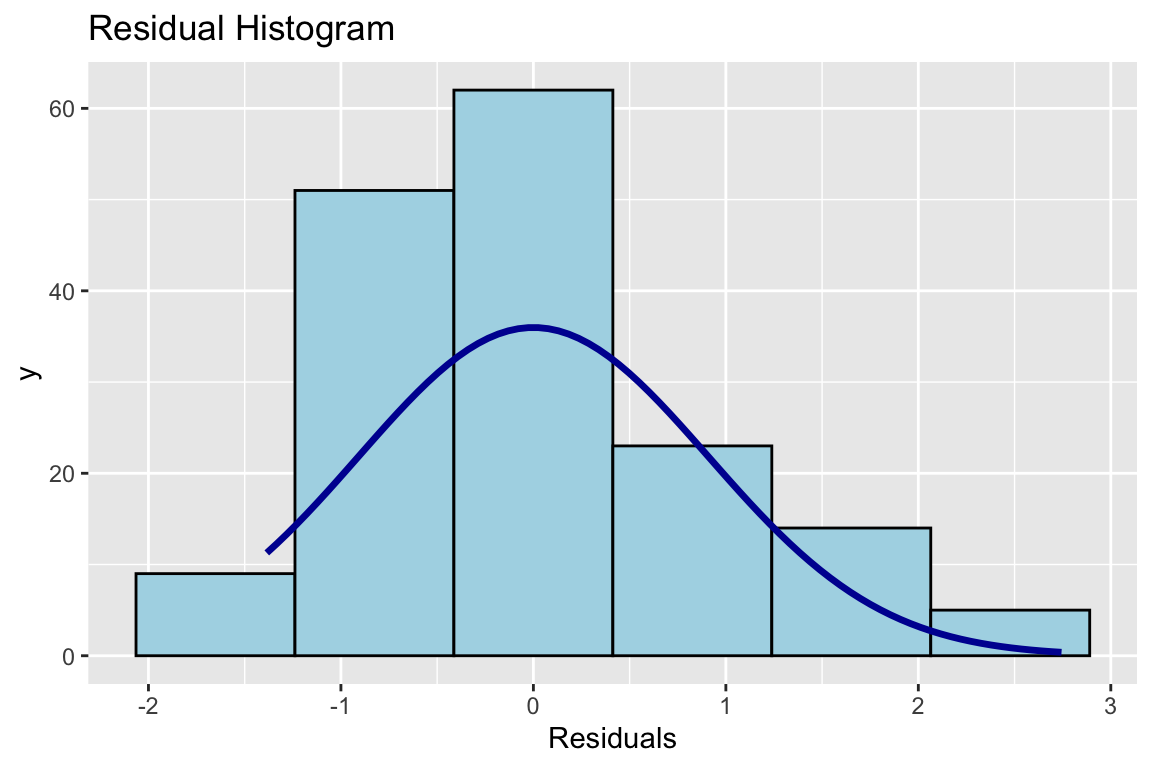
Histogramm der Residuen
Ü1.13 Jetzt auf Normalverteilung testen
# Führe Tests auf signifikante Verletzungen
# der Normalverteilungsannahme aus.
olsrr::ols_test_normality(Modell1)
## -----------------------------------------------
## Test Statistic pvalue
## -----------------------------------------------
## Shapiro-Wilk 0.9349 0.0000
## Kolmogorov-Smirnov 0.127 0.0101
## Cramer-von Mises 15.381 0.0000
## Anderson-Darling 3.2969 0.0000
## -----------------------------------------------Ü1.14 Fazit
Was ist Ihr Fazit aus der Regressionsrechnung?
Weiterführung
| Predictors | B | BETA | std.err | t | p |
|---|---|---|---|---|---|
| (Intercept) | 1.57 | 0.32 | 4.89 | <.001 | |
| E102_02 | 0.47 | .480 | 0.07 | 6.71 | <.001 |
| E102_04 | -0.06 | -.076 | 0.06 | -1.06 | .292 |
| a R² = 0.25 (F = 28, df = 161, p = 161), R²adj. = 0.25 |
Take Home – Ausblick – Vokabeln
Take Home
Note
- Sie können eine Regressionsanalyse in Quarto berechnen und die Ergebnisse interpretieren
- Ihnen ist klar, was es bedeutet, dass Dritteinflüsse herausgerechnet werden.
- Sie können Residualanalysen anschauen und erkennen, wann es Probleme gibt (mögliche Lösungen kommen später)
- Sie können den notwendigen Code für Regressionsanalysen in Ihre Projekte kopieren und an den richtigen Stellen anpassen.
Ausblick
Wie beschäftigen uns mit kategorialen Variablen in den UVs.
Vokabeln 🔗
:::

Fretwurst | Statistik Aufbau: GLM – BLUE
