13 Fokussierte Zusammenfassung
Die Folien zur Sitzung
Vodcast Zusammenfassung
(Unter dem Video auf Youtube.com finden Sie das Inhaltsverzeichnis ebenfalls verlinkt.)Einstieg
00:08 Hinweise zur Prüfung
12:06 - Intro und Überblick über die erlernten Verfahren
Bivariates
25:28 - Covarianz und Korrelation
29:16 - Regression bivariat
34:01 - b’s (bivariat)
36:50 - BETAs bivariat
42:32 - Standardfehler der b’s bivariat
46:35 - R² Modellgüte bivariat
54:47 - t-Tests der b’s bivariat
57:02 - R-Output Regression bivariat
Multivariates lineares Modell (GLM)
01:01:51 - Multivariate Regression
01:07:29 - OLS
01:08:54 - b’s multivariat
Voraussetzungen OLS
01:14:23 - Voraussetzungen OLS für BLUE
01:20:11 - Multikollinearität
01:26:19 - Lineartransformation
01:27:45 - Heteroskedastizität
01:30:53 - Residualverteilung
Dummys als UV
01:32:28 - Dummy UVs
01:42:07 - Slope-Dummys
Interaktionen
01:52:25 - Interaktion zweier metrischer
Weitere Analysemethoden
01:54:15 - Faktorenanalysen
02:09:43 - Logistische Regression
02:18:15 - Machine Learning ML
02:20:11 - Clusteranalysen
02:35:49 - Nächste Woche
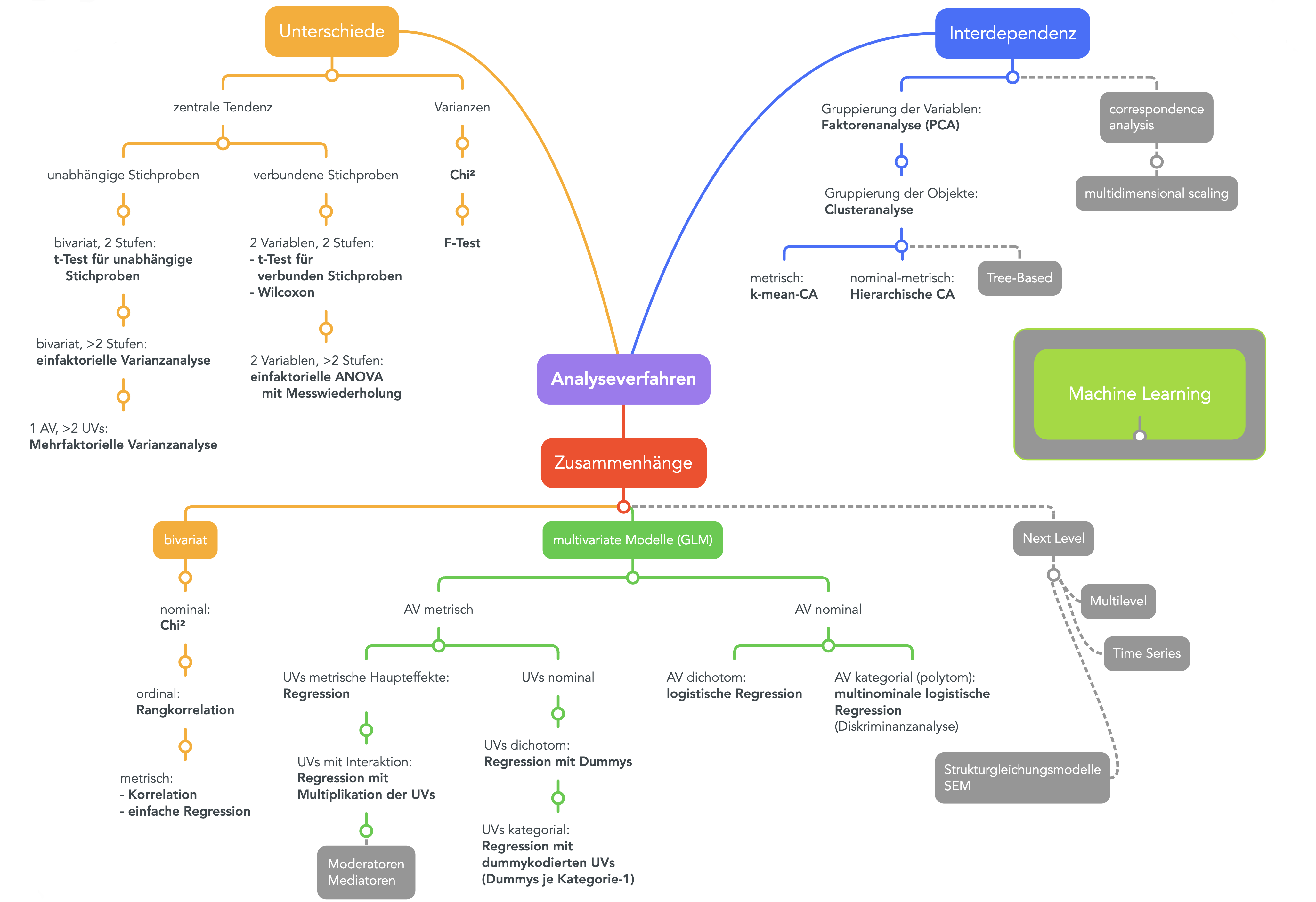
Die verschiedenen Analysemethoden, die Sie in diesem Semester kennengelernt haben, ermöglichen es, Daten aus unterschiedlichen Blickwinkeln zu analysieren. Man kann also mit denselben Variablen eine Zusammenhangsanalyse machen oder sie auf Unterschiede hin analysieren oder schauen, ob es Interdependenzen gibt, sie als Gruppen bilden. Die zugrundeliegenden Beziehungen in den Daten sind natürlich immer dieselben. Das liegt daran, dass Unterschiede durch Zusammenhänge entstehen und Zusammenhänge aufgrund von Unterschieden. Beides finden seine Ursache darin, dass Variablen und Fälle Gruppen bilden; und gleichzeitig entstehen die Gruppen durch die Zusammenhänge und Unterschiede.
Die Kennwerte, die aufgrund von Unterschiedsanalysen entstehen sind nicht sehr hoch verdichtet. Daher sind sie leichter zu lernen und für den Einstieg in die Statistik gut geeignet. Sie haben bereits Unterschiedsanalysen kennengelernt, die Masse (gesprochen Maße :-) der zentralen Tendenz auswerten, also zum Beispiel den t-Test für Mittelwertunterschiede zwischen zwei Gruppen. Wir können dabei Variablen aus verschiedenen Teilstichproben (Gruppe der Wähler:innen und Nichtwähler:innen) untersuchen, also «unabhängige Stichproben». Oder wir untersuchen «verbundene Stichproben», wenn zum Beispiel die Mittelwerte von zwei Variablen verglichen werden sollen, die jeweils für die ganze Stichprobe erhoben wurden (zB vor und nach einem experimentellem Eingriff aka Treatment). Oder wir untersuchen die Varianzen von Variablen mit Hilfe von \(\chi^2\) oder einem F-Test.
Wenn Sie genau auf die Grafik schauen, finden Sie den \(\chi^2\) -Test einmal bei den Unterschieden und einmal bei den «bivariaten» Zusammenhangsanalysen. Das liegt an der oben angesprochenen Verbundenheit der Konzepte: Unterschiede entstehen, wenn Dinge miteinander zusmamenhängen. Bei den Zusammenhangsanyalysen unterscheiden wir die «bivariten» von den «multivariten Modellen». Die bivariten bringen nur zwei Variablen in Beziehung zueinander, was sie einfacher macht, aber im Grunde zu einfach, um die komplexeren Zusammenhänge in unserer Welt zu erklären. Menschen sind einfach nicht bivariat und unsere Welt ist nicht monokausal. Die multivariaten Modelle sind Erweiterungen der bivariaten Analysemethoden. Bei den «Generalisierten Linearen Modellen» (GLM) geht es also weiter. Analysestrategien der GLM werden nach den Skalenniveaus der Variablen unterschieden, die erklärt werden sollen (also die abhängigen Variablen aka AV) und nach den Skalenniveaus der erklärenden (unabhängigen Variablen aka UV).
Die Analysemethoden sind dann einfacher, wenn das Skalenniveau hoch ist. Darum machen wir den Einstieg auch mit der Regression, bei der die AV und die UVs metrisch sind. Wenn die UVs nominal sind (bzw. nominale vorkommen), wird oft auch von Varianzanalysen (Analysis of Variance aka ANOVA) gesprochen. Wenn die AV nominal ist (dichotom oder polytom) werden logistische Regressionen gerechnet. Wenn Sie nach dem Bachelorstudium mit dem Master weitermachen, lernen Sie die multivariaten Analysemethoden auf dem «Next Level» kennen – also zumindest einige davon. Wenn Sie dann auch noch in die Wissenschaft weitergehen, befassen Sie sich sicher spezialisierter mit bestimmten Verfahren der statistischen Datenanalyse, die für Ihre Forschung die am besten geeignete ist.
In diesem Semester werden wir uns auch mit Verfahren befassen, die Gruppierungen (aka Interdependenzen) untersuchen. Dazu gehört an erster Stelle die Faktorenanalyse, mit deren Hilfe Faktoren extrahiert werden sollen, die – so die Vermutung – die gemeinsame Ursache für gemessene Variablen sind. Die Idee ist also, dass manifest gemessene Variablen aufgrund von latenten Variablen miteinander zusammenhängen beziehungsweise korrelieren. Das ist schon an sich interessant genug. Darüber hinausgehend, können wir mit Hilfe einer Faktorenanalyse Indizes bauen, die mehrere Variablen auf einmal abbilden. Während die Faktorenanalyse Eigenschaften von Fällen auf zugrundeliegende Gemeinsamkeiten hin untersucht, werden mit Clusteranalysen Fallgruppen gebildet. Zum Beispiel könnten wir untersuchen, ob die Begeisterung und Abneigung gegenüber Mathemaitik, Statistik, Computer-Programmierung, R usw. einen gemeinsamen Kern haben, wie schlechter Matheunterricht oder Identitiätsbildung. Und dann könnten wir mit Clusteranalysen Gruppen identifizieren, je nachdem, wie gross die Begeisterung für Mathe is, für Computer und für Programmiersprachen wie R. Da gibt es sicher die einen und die anderen. Solche, die tollen Matheunterricht hatten und trotzdem mit R auf Kriegsfuss stehen usw. Also, Sie sehen, wir können viel damit anstellen. Das lohnt sich, auch wenn der Weg teils beschwerlich ist.