# Prüfe, ob es in dem Ordner in der die Uebung_2.qmd gespeichert ist, folgende Unterordner gibt und wenn nicht, dann lege sie an
if(dir.exists("files")){} else {dir.create("files")}
if(dir.exists("data")){} else {dir.create("data")}
if(dir.exists("images")){} else {dir.create("images")}
# lade die _common.R und speichere sie im Ordner "files"
download.file("https://stat.ikmz.uzh.ch/Aufbau/Folien/Sitzung_06/files/_common.R", destfile= "_common.R")
# Wenn die folgenen Pakete jeweils nicht schon installiert sind, werden sie installiert
if (!require("devtools")) install.packages("devtools")
if(!require("corrr")) install.packages("corrr")
if(!require("kableExtra")) install.packages("kableExtra")
if(!require("psych")) install.package("psych")
# jetzt noch die Problembär-Pakete forcierter installieren.
# Wenn die Nachricht kommt, das die Pakete seit der letzten Installation nicht geändert wurden und daher geskippt werden, is das perfekt in Ordnung
if(!require("sjmisc"))devtools::install_github("strengejacke/sjmisc")9 Übung: Dimensionsreduktion
9.1 Die Folien zur Sitzung
Hier die Uebung_03.qmd zum Download.
Vorbereitungen
Der folgende R-Chunk soll Ihnen bei der Installation von benötigten Paketen helfen und eine geeignete Dateistruktur anlegen, wenn sie nicht schon da ist. Speichern Sie die qmd-Datei in einem Ordner auf Ihrem Rechner ab (am besten in einem Ordner mit Cloudsynchronisation wie Dropbox, SWITCH oder oneDrive). Wenn Sie den folgenden Chunk ausführen, werden Ihnen in dem Ordner die Unterordner «files», «data», und «images» angelegt (wenn sie nicht schon da sind und im Fall unangetastet bleiben). Dann wird die _common.R heruntergeladen, in der ein paar Optionen gespeichert sind. Wenn Sie daran Änderungen vornehmen und diese für später behalten möchten, müssen Sie die Zeile mit «download.file…» beginnt auskommentieren (# davor).
Versuchen Sie die folgenden Zeilen zu verstehen und führen Sie die Befehle aus. Wenn Sie etwas nicht verstehen, googlen Sie die Pakte (zB «r corrr») und schauen sich dort die Vignette des Paketes an.
Mit dem Die Installation von benötigten Paketen ist weiter vereinfacht.
Übung 3
3.0 Laden Sie die Daten unserer Befragung
(Für den Fall, dass es Probleme gibt, laden Sie die Daten hier herunter. Wenn das auch zu Problemen führt, melden Sie sich im Forum.)
# tidyverse laden
suppressPackageStartupMessages(library("tidyverse"))
# Wenn wir die Dateien einmal geladen und aufbereitet haben (mit der Extradatei "Aufbereitung.qmd"), dann ist es besser, nicht immer wieder neu die Rohdaten zu laden, sondern die Aufbereiteten.
# Prüfe, ob es in dem Ordner in der die Uebung_1_ab.qmd gespeichert ist, einen Unterordner "files" gibt und, wenn nicht, dann lege ihn an.
if(dir.exists("data")){invisible()} else {dir.create("data")}
download.file("https://stat.ikmz.uzh.ch/Aufbau/Folien/Sitzung_04/data/Stat_Aufbau_Befragung.RDS", "data/Stat_Aufbau_Befragung.RDS")
DATEN <- readRDS("data/Stat_Aufbau_Befragung.RDS") |>
haven::zap_formats()
# DATEN |> sjlabelled::get_label()
DATEN |>
saveRDS("data/Stat_Aufbau_Befragung.RDS")Führen Sie eine Faktorenanalyse für unsere RAQ aus mit Hilfe des Paketes psych
Ziehen Sie dazu die Hilfe dieser Website heran: https://md.psych.bio.uni-goettingen.de/mv/unit/fa/efa.html
3.1 Schauen Sie sich die Korrelationsmatrix (mit cor()) an.
3.2 Führen Sie einen Bartlett’s-Test aus
3.3 Führen Sie einen KMO-Test aus (psych::KMO())
3.4. Machen Sie eine Parallel-Analyse (psych::fa.parallel()), um die Anzahl der Faktoren zu bestimmen.
3.5. Führen Sie eine Faktorenanalyse durch mit psych::fa() und rotieren Sie mit rotate = "promax". 5.1. Schauen Sie sich die Faktorladungen an. 5.2. Wie viel Varianz erklären die Faktoren?
3.6. Erstellen Sie ein Diagramm für die Faktorenanalyse (psych::fa.diagramm).
3.7. Führen Sie eine Faktorenanalyse mit Rotation nach dem Kriterium rotate = "oblimin" durch.
«psych» laden
Das Paket psych brauchen wir im Folgenden mehrfach. Es kann für die Sitzung mit Hilfe von library()-funktion geladen werden. Danach braucht man eigentlich nicht mehr immer psych:: vor jede Funktion schreiben, aber ich empfehle es und der Styleguide von R-Studio auch. Dann weiss man 1. immer, welches Paket gerade verwendet wird bei einer Funktion (für andere ist das auch deutlich leichter lesbar). 2. kann man sicher sein, dass es keine Konflikte gibt, weil zB mehrere Pakete die Funktion filter verwenden und 3. braucht man eben nicht mehr irgendwo am Anfang die ganzen Pakete mit library laden. Also, den Aufruf kann man machen, muss aber nicht.
##
## Attaching package: 'psych'
## The following objects are masked from 'package:ggplot2':
##
## %+%, alphaOrientierung in den Daten
Schauen Sie in den Fragebogen, welche Variablen zur RAQ-Skala gehören: FB_STATA.pdf (uzh.ch)
Dann rufen Sie immer vor einer höheren Analyse die Häufigkeitstabellen einmal auf und schauen sich die Variablen an. Was haben sie für einen Range? Gibt es Werte in den Variablen, die eigentlich nicht sein können (zB sind befragte teils über 2000 Jahre als)? Wie viele fehlende Werte (NA) haben die Variablen? Gibt es zB negative Variablen (-9) die als Wert mitverarbeitet werden, aber eigentlich für einen fehlenden Wert (Missing stehen)? Also:
## RAQ: Statistik bringt mich zum Weinen. (R101_01) <integer>
## # total N=167 valid N=167 mean=2.95 sd=1.34
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 29 | 17.37 | 17.37 | 17.37
## 2 | 2 | 42 | 25.15 | 25.15 | 42.51
## 3 | 3 | 30 | 17.96 | 17.96 | 60.48
## 4 | 4 | 41 | 24.55 | 24.55 | 85.03
## 5 | 5 trifft voll und ganz zu | 25 | 14.97 | 14.97 | 100.00
## <NA> | <NA> | 0 | 0.00 | <NA> | <NA>
##
## RAQ: Meine Freunde werden denken, ich sei dumm, weil ich nicht mit R umgehen kann. (R101_02) <integer>
## # total N=167 valid N=166 mean=1.83 sd=1.09
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 86 | 51.50 | 51.81 | 51.81
## 2 | 2 | 45 | 26.95 | 27.11 | 78.92
## 3 | 3 | 17 | 10.18 | 10.24 | 89.16
## 4 | 4 | 13 | 7.78 | 7.83 | 96.99
## 5 | 5 trifft voll und ganz zu | 5 | 2.99 | 3.01 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Standardabweichungen begeistern mich. (R101_03) <integer>
## # total N=167 valid N=166 mean=1.94 sd=0.93
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 63 | 37.72 | 37.95 | 37.95
## 2 | 2 | 62 | 37.13 | 37.35 | 75.30
## 3 | 3 | 31 | 18.56 | 18.67 | 93.98
## 4 | 4 | 8 | 4.79 | 4.82 | 98.80
## 5 | 5 trifft voll und ganz zu | 2 | 1.20 | 1.20 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich träume davon, dass Pearson mich mit Korrelationskoeffizienten angreift. (R101_04) <integer>
## # total N=167 valid N=166 mean=1.83 sd=1.27
##
## Value | Label | N | Raw % | Valid % | Cum. %
## --------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 102 | 61.08 | 61.45 | 61.45
## 2 | 2 | 27 | 16.17 | 16.27 | 77.71
## 3 | 3 | 14 | 8.38 | 8.43 | 86.14
## 4 | 4 | 10 | 5.99 | 6.02 | 92.17
## 5 | 5 trifft voll und ganz zu | 13 | 7.78 | 7.83 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich verstehe Statistik nicht. (R101_05) <integer>
## # total N=167 valid N=166 mean=2.81 sd=1.14
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 21 | 12.57 | 12.65 | 12.65
## 2 | 2 | 48 | 28.74 | 28.92 | 41.57
## 3 | 3 | 52 | 31.14 | 31.33 | 72.89
## 4 | 4 | 31 | 18.56 | 18.67 | 91.57
## 5 | 5 trifft voll und ganz zu | 14 | 8.38 | 8.43 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich habe wenig Erfahrung mit Computern. (R101_06) <integer>
## # total N=167 valid N=166 mean=2.63 sd=1.16
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 33 | 19.76 | 19.88 | 19.88
## 2 | 2 | 47 | 28.14 | 28.31 | 48.19
## 3 | 3 | 41 | 24.55 | 24.70 | 72.89
## 4 | 4 | 38 | 22.75 | 22.89 | 95.78
## 5 | 5 trifft voll und ganz zu | 7 | 4.19 | 4.22 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Alle Computer hassen mich. (R101_07) <integer>
## # total N=167 valid N=167 mean=1.94 sd=1.20
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 87 | 52.10 | 52.10 | 52.10
## 2 | 2 | 31 | 18.56 | 18.56 | 70.66
## 3 | 3 | 31 | 18.56 | 18.56 | 89.22
## 4 | 4 | 8 | 4.79 | 4.79 | 94.01
## 5 | 5 trifft voll und ganz zu | 10 | 5.99 | 5.99 | 100.00
## <NA> | <NA> | 0 | 0.00 | <NA> | <NA>
##
## RAQ: Ich war noch nie gut in Mathe. (R101_08) <integer>
## # total N=167 valid N=166 mean=2.66 sd=1.22
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 32 | 19.16 | 19.28 | 19.28
## 2 | 2 | 51 | 30.54 | 30.72 | 50.00
## 3 | 3 | 40 | 23.95 | 24.10 | 74.10
## 4 | 4 | 28 | 16.77 | 16.87 | 90.96
## 5 | 5 trifft voll und ganz zu | 15 | 8.98 | 9.04 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Meine Freunde sind besser in Statistik als ich. (R101_09) <integer>
## # total N=167 valid N=166 mean=2.95 sd=1.07
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 12 | 7.19 | 7.23 | 7.23
## 2 | 2 | 46 | 27.54 | 27.71 | 34.94
## 3 | 3 | 62 | 37.13 | 37.35 | 72.29
## 4 | 4 | 30 | 17.96 | 18.07 | 90.36
## 5 | 5 trifft voll und ganz zu | 16 | 9.58 | 9.64 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Computer sind nur zum Spielen nützlich. (R101_10) <integer>
## # total N=167 valid N=166 mean=1.65 sd=0.98
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 98 | 58.68 | 59.04 | 59.04
## 2 | 2 | 43 | 25.75 | 25.90 | 84.94
## 3 | 3 | 16 | 9.58 | 9.64 | 94.58
## 4 | 4 | 3 | 1.80 | 1.81 | 96.39
## 5 | 5 trifft voll und ganz zu | 6 | 3.59 | 3.61 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich war in der Schule schlecht in Mathematik. (R101_11) <integer>
## # total N=167 valid N=167 mean=2.84 sd=1.28
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 32 | 19.16 | 19.16 | 19.16
## 2 | 2 | 36 | 21.56 | 21.56 | 40.72
## 3 | 3 | 45 | 26.95 | 26.95 | 67.66
## 4 | 4 | 35 | 20.96 | 20.96 | 88.62
## 5 | 5 trifft voll und ganz zu | 19 | 11.38 | 11.38 | 100.00
## <NA> | <NA> | 0 | 0.00 | <NA> | <NA>
##
## RAQ: Leute versuchen dir zu sagen, dass R die Statistik leichter verständlich macht, aber das stimmt nicht. (R101_12) <integer>
## # total N=167 valid N=166 mean=3.00 sd=1.25
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 24 | 14.37 | 14.46 | 14.46
## 2 | 2 | 35 | 20.96 | 21.08 | 35.54
## 3 | 3 | 46 | 27.54 | 27.71 | 63.25
## 4 | 4 | 39 | 23.35 | 23.49 | 86.75
## 5 | 5 trifft voll und ganz zu | 22 | 13.17 | 13.25 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich mache mir Sorgen, dass ich wegen meiner Inkompetenz mit Computern irreparable Schäden verursachen werde. (R101_13) <integer>
## # total N=167 valid N=166 mean=1.77 sd=1.12
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 95 | 56.89 | 57.23 | 57.23
## 2 | 2 | 38 | 22.75 | 22.89 | 80.12
## 3 | 3 | 16 | 9.58 | 9.64 | 89.76
## 4 | 4 | 10 | 5.99 | 6.02 | 95.78
## 5 | 5 trifft voll und ganz zu | 7 | 4.19 | 4.22 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Computer haben ihren eigenen Willen und gehen absichtlich immer dann kaputt, wenn ich sie benutze. (R101_14) <integer>
## # total N=167 valid N=166 mean=1.56 sd=0.96
##
## Value | Label | N | Raw % | Valid % | Cum. %
## --------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 110 | 65.87 | 66.27 | 66.27
## 2 | 2 | 33 | 19.76 | 19.88 | 86.14
## 3 | 3 | 14 | 8.38 | 8.43 | 94.58
## 4 | 4 | 4 | 2.40 | 2.41 | 96.99
## 5 | 5 trifft voll und ganz zu | 5 | 2.99 | 3.01 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Computer sind darauf aus, mich zu überlisten. (R101_15) <integer>
## # total N=167 valid N=166 mean=1.52 sd=0.94
##
## Value | Label | N | Raw % | Valid % | Cum. %
## --------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 112 | 67.07 | 67.47 | 67.47
## 2 | 2 | 36 | 21.56 | 21.69 | 89.16
## 3 | 3 | 10 | 5.99 | 6.02 | 95.18
## 4 | 4 | 2 | 1.20 | 1.20 | 96.39
## 5 | 5 trifft voll und ganz zu | 6 | 3.59 | 3.61 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich weine offen, wenn von zentraler Tendenz die Rede ist. (R101_16) <integer>
## # total N=167 valid N=166 mean=2.02 sd=1.29
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 84 | 50.30 | 50.60 | 50.60
## 2 | 2 | 33 | 19.76 | 19.88 | 70.48
## 3 | 3 | 22 | 13.17 | 13.25 | 83.73
## 4 | 4 | 15 | 8.98 | 9.04 | 92.77
## 5 | 5 trifft voll und ganz zu | 12 | 7.19 | 7.23 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich falle in ein Koma, wenn ich eine Gleichung sehe. (R101_17) <integer>
## # total N=167 valid N=166 mean=1.86 sd=1.16
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 88 | 52.69 | 53.01 | 53.01
## 2 | 2 | 41 | 24.55 | 24.70 | 77.71
## 3 | 3 | 19 | 11.38 | 11.45 | 89.16
## 4 | 4 | 9 | 5.39 | 5.42 | 94.58
## 5 | 5 trifft voll und ganz zu | 9 | 5.39 | 5.42 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: R stürzt immer ab, wenn ich versuche, es zu benutzen. (R101_18) <integer>
## # total N=167 valid N=166 mean=1.74 sd=1.07
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 94 | 56.29 | 56.63 | 56.63
## 2 | 2 | 42 | 25.15 | 25.30 | 81.93
## 3 | 3 | 15 | 8.98 | 9.04 | 90.96
## 4 | 4 | 9 | 5.39 | 5.42 | 96.39
## 5 | 5 trifft voll und ganz zu | 6 | 3.59 | 3.61 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Alle schauen mich an, wenn ich R benutze. (R101_19) <integer>
## # total N=167 valid N=166 mean=1.52 sd=0.98
##
## Value | Label | N | Raw % | Valid % | Cum. %
## --------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 117 | 70.06 | 70.48 | 70.48
## 2 | 2 | 26 | 15.57 | 15.66 | 86.14
## 3 | 3 | 13 | 7.78 | 7.83 | 93.98
## 4 | 4 | 5 | 2.99 | 3.01 | 96.99
## 5 | 5 trifft voll und ganz zu | 5 | 2.99 | 3.01 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich kann nicht schlafen, weil ich an Signifikanzen denke. (R101_20) <integer>
## # total N=167 valid N=166 mean=1.87 sd=1.26
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 97 | 58.08 | 58.43 | 58.43
## 2 | 2 | 29 | 17.37 | 17.47 | 75.90
## 3 | 3 | 16 | 9.58 | 9.64 | 85.54
## 4 | 4 | 13 | 7.78 | 7.83 | 93.37
## 5 | 5 trifft voll und ganz zu | 11 | 6.59 | 6.63 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich wache unter meiner Bettdecke auf und denke, dass ich unter einer Normalverteilung gefangen bin. (R101_21) <integer>
## # total N=167 valid N=166 mean=1.93 sd=1.41
##
## Value | Label | N | Raw % | Valid % | Cum. %
## --------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 104 | 62.28 | 62.65 | 62.65
## 2 | 2 | 16 | 9.58 | 9.64 | 72.29
## 3 | 3 | 18 | 10.78 | 10.84 | 83.13
## 4 | 4 | 9 | 5.39 | 5.42 | 88.55
## 5 | 5 trifft voll und ganz zu | 19 | 11.38 | 11.45 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Meine Freunde sind besser in R als ich. (R101_22) <integer>
## # total N=167 valid N=166 mean=2.86 sd=1.15
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 19 | 11.38 | 11.45 | 11.45
## 2 | 2 | 48 | 28.74 | 28.92 | 40.36
## 3 | 3 | 54 | 32.34 | 32.53 | 72.89
## 4 | 4 | 28 | 16.77 | 16.87 | 89.76
## 5 | 5 trifft voll und ganz zu | 17 | 10.18 | 10.24 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Wenn ich gut in Statistik bin, werden die Leute denken, ich sei ein Streber. (R101_23) <integer>
## # total N=167 valid N=166 mean=1.92 sd=1.28
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 96 | 57.49 | 57.83 | 57.83
## 2 | 2 | 25 | 14.97 | 15.06 | 72.89
## 3 | 3 | 18 | 10.78 | 10.84 | 83.73
## 4 | 4 | 17 | 10.18 | 10.24 | 93.98
## 5 | 5 trifft voll und ganz zu | 10 | 5.99 | 6.02 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich mag Statistik, würde das aber nie vor meinen Freunden zugeben. (R101_24) <integer>
## # total N=167 valid N=166 mean=1.53 sd=0.90
##
## Value | Label | N | Raw % | Valid % | Cum. %
## --------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 111 | 66.47 | 66.87 | 66.87
## 2 | 2 | 32 | 19.16 | 19.28 | 86.14
## 3 | 3 | 16 | 9.58 | 9.64 | 95.78
## 4 | 4 | 4 | 2.40 | 2.41 | 98.19
## 5 | 5 trifft voll und ganz zu | 3 | 1.80 | 1.81 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>3.1 Korrelationstabelle
Erste Versuche, die nicht funktionieren:
R-Code
# geht nicht:
DATEN |>
cor(R101_01:R101_24)
# geht auch nicht:
head(round(cor(DATEN$R101_01:DATEN$R101_24), 2))So geht es:
Ich lege ein neues Datenset «items» an, das gebildet (<-) wird indem
1. die Daten genommen werden |> 2. die Variablen ausgewählt werden, die miteinander korreliert werden sollen |> 3. Fehlende Werte (NA) ausgelassen werden (omit) mit der Funktion na.omit()
Also:
R-Code
# erstmal die items extrahieren
items <- DATEN |>
select(R101_01:R101_24) |>
na.omit() # sorgt dafür, dass keine NAs mehr in den Daten sind
# jetzt funktioniert die Vorlage:
round(cor(items), 2)
## R101_01 R101_02 R101_03 R101_04 R101_05 R101_06 R101_07 R101_08 R101_09
## R101_01 1.00 0.36 -0.25 0.13 0.58 0.30 0.37 0.35 0.40
## R101_02 0.36 1.00 0.02 0.19 0.39 0.38 0.37 0.15 0.22
## R101_03 -0.25 0.02 1.00 0.11 -0.23 -0.01 0.00 -0.21 -0.14
## R101_04 0.13 0.19 0.11 1.00 0.20 -0.22 0.11 0.04 0.27
## R101_05 0.58 0.39 -0.23 0.20 1.00 0.39 0.37 0.40 0.42
## R101_06 0.30 0.38 -0.01 -0.22 0.39 1.00 0.44 0.17 0.07
## R101_07 0.37 0.37 0.00 0.11 0.37 0.44 1.00 0.17 0.15
## R101_08 0.35 0.15 -0.21 0.04 0.40 0.17 0.17 1.00 0.44
## R101_09 0.40 0.22 -0.14 0.27 0.42 0.07 0.15 0.44 1.00
## R101_10 0.20 0.18 0.00 0.17 0.20 0.16 0.36 -0.03 0.17
## R101_11 0.20 0.04 -0.12 0.04 0.25 0.01 0.03 0.76 0.39
## R101_12 0.38 0.33 -0.14 0.04 0.45 0.35 0.51 0.28 0.17
## R101_13 0.29 0.52 0.07 0.13 0.36 0.41 0.57 0.16 0.17
## R101_14 0.19 0.41 0.02 0.15 0.21 0.31 0.51 0.05 0.07
## R101_15 0.21 0.46 0.08 0.12 0.18 0.31 0.53 0.06 0.08
## R101_16 0.49 0.20 -0.05 0.28 0.41 0.19 0.49 0.23 0.21
## R101_17 0.24 0.12 -0.19 0.27 0.30 0.12 0.33 0.26 0.16
## R101_18 0.32 0.24 0.02 0.07 0.31 0.28 0.46 0.04 0.08
## R101_19 0.07 0.11 0.12 0.28 0.14 0.13 0.24 0.01 0.02
## R101_20 0.28 0.32 0.03 0.45 0.40 0.17 0.32 0.13 0.18
## R101_21 0.18 0.19 0.03 0.56 0.18 0.02 0.30 0.08 0.07
## R101_22 0.40 0.24 -0.21 0.17 0.39 0.19 0.15 0.35 0.67
## R101_23 0.01 0.06 0.03 0.09 -0.07 -0.12 0.07 -0.25 -0.03
## R101_24 -0.17 0.05 0.31 0.19 -0.12 -0.06 0.10 -0.22 -0.13
## R101_10 R101_11 R101_12 R101_13 R101_14 R101_15 R101_16 R101_17 R101_18
## R101_01 0.20 0.20 0.38 0.29 0.19 0.21 0.49 0.24 0.32
## R101_02 0.18 0.04 0.33 0.52 0.41 0.46 0.20 0.12 0.24
## R101_03 0.00 -0.12 -0.14 0.07 0.02 0.08 -0.05 -0.19 0.02
## R101_04 0.17 0.04 0.04 0.13 0.15 0.12 0.28 0.27 0.07
## R101_05 0.20 0.25 0.45 0.36 0.21 0.18 0.41 0.30 0.31
## R101_06 0.16 0.01 0.35 0.41 0.31 0.31 0.19 0.12 0.28
## R101_07 0.36 0.03 0.51 0.57 0.51 0.53 0.49 0.33 0.46
## R101_08 -0.03 0.76 0.28 0.16 0.05 0.06 0.23 0.26 0.04
## R101_09 0.17 0.39 0.17 0.17 0.07 0.08 0.21 0.16 0.08
## R101_10 1.00 -0.09 0.21 0.31 0.32 0.33 0.18 0.07 0.03
## R101_11 -0.09 1.00 0.19 0.08 -0.03 -0.09 0.11 0.23 0.08
## R101_12 0.21 0.19 1.00 0.42 0.23 0.28 0.33 0.22 0.28
## R101_13 0.31 0.08 0.42 1.00 0.50 0.58 0.35 0.29 0.37
## R101_14 0.32 -0.03 0.23 0.50 1.00 0.71 0.30 0.24 0.35
## R101_15 0.33 -0.09 0.28 0.58 0.71 1.00 0.30 0.31 0.39
## R101_16 0.18 0.11 0.33 0.35 0.30 0.30 1.00 0.54 0.22
## R101_17 0.07 0.23 0.22 0.29 0.24 0.31 0.54 1.00 0.34
## R101_18 0.03 0.08 0.28 0.37 0.35 0.39 0.22 0.34 1.00
## R101_19 0.05 0.04 0.09 0.36 0.17 0.31 0.22 0.31 0.41
## R101_20 0.20 0.18 0.19 0.35 0.36 0.29 0.42 0.44 0.37
## R101_21 0.25 0.10 0.16 0.28 0.34 0.31 0.32 0.40 0.38
## R101_22 0.26 0.29 0.26 0.15 0.08 0.09 0.21 0.18 0.16
## R101_23 0.12 -0.23 -0.12 0.15 0.25 0.21 0.04 0.11 0.12
## R101_24 0.08 -0.23 -0.16 0.13 0.20 0.25 0.04 0.13 0.10
## R101_19 R101_20 R101_21 R101_22 R101_23 R101_24
## R101_01 0.07 0.28 0.18 0.40 0.01 -0.17
## R101_02 0.11 0.32 0.19 0.24 0.06 0.05
## R101_03 0.12 0.03 0.03 -0.21 0.03 0.31
## R101_04 0.28 0.45 0.56 0.17 0.09 0.19
## R101_05 0.14 0.40 0.18 0.39 -0.07 -0.12
## R101_06 0.13 0.17 0.02 0.19 -0.12 -0.06
## R101_07 0.24 0.32 0.30 0.15 0.07 0.10
## R101_08 0.01 0.13 0.08 0.35 -0.25 -0.22
## R101_09 0.02 0.18 0.07 0.67 -0.03 -0.13
## R101_10 0.05 0.20 0.25 0.26 0.12 0.08
## R101_11 0.04 0.18 0.10 0.29 -0.23 -0.23
## R101_12 0.09 0.19 0.16 0.26 -0.12 -0.16
## R101_13 0.36 0.35 0.28 0.15 0.15 0.13
## R101_14 0.17 0.36 0.34 0.08 0.25 0.20
## R101_15 0.31 0.29 0.31 0.09 0.21 0.25
## R101_16 0.22 0.42 0.32 0.21 0.04 0.04
## R101_17 0.31 0.44 0.40 0.18 0.11 0.13
## R101_18 0.41 0.37 0.38 0.16 0.12 0.10
## R101_19 1.00 0.42 0.43 0.14 0.19 0.19
## R101_20 0.42 1.00 0.64 0.16 0.11 0.23
## R101_21 0.43 0.64 1.00 0.15 0.15 0.22
## R101_22 0.14 0.16 0.15 1.00 0.08 -0.11
## R101_23 0.19 0.11 0.15 0.08 1.00 0.45
## R101_24 0.19 0.23 0.22 -0.11 0.45 1.00
# Schöner ist aber mit Pipes:
items |>
cor() |>
round(2)
## R101_01 R101_02 R101_03 R101_04 R101_05 R101_06 R101_07 R101_08 R101_09
## R101_01 1.00 0.36 -0.25 0.13 0.58 0.30 0.37 0.35 0.40
## R101_02 0.36 1.00 0.02 0.19 0.39 0.38 0.37 0.15 0.22
## R101_03 -0.25 0.02 1.00 0.11 -0.23 -0.01 0.00 -0.21 -0.14
## R101_04 0.13 0.19 0.11 1.00 0.20 -0.22 0.11 0.04 0.27
## R101_05 0.58 0.39 -0.23 0.20 1.00 0.39 0.37 0.40 0.42
## R101_06 0.30 0.38 -0.01 -0.22 0.39 1.00 0.44 0.17 0.07
## R101_07 0.37 0.37 0.00 0.11 0.37 0.44 1.00 0.17 0.15
## R101_08 0.35 0.15 -0.21 0.04 0.40 0.17 0.17 1.00 0.44
## R101_09 0.40 0.22 -0.14 0.27 0.42 0.07 0.15 0.44 1.00
## R101_10 0.20 0.18 0.00 0.17 0.20 0.16 0.36 -0.03 0.17
## R101_11 0.20 0.04 -0.12 0.04 0.25 0.01 0.03 0.76 0.39
## R101_12 0.38 0.33 -0.14 0.04 0.45 0.35 0.51 0.28 0.17
## R101_13 0.29 0.52 0.07 0.13 0.36 0.41 0.57 0.16 0.17
## R101_14 0.19 0.41 0.02 0.15 0.21 0.31 0.51 0.05 0.07
## R101_15 0.21 0.46 0.08 0.12 0.18 0.31 0.53 0.06 0.08
## R101_16 0.49 0.20 -0.05 0.28 0.41 0.19 0.49 0.23 0.21
## R101_17 0.24 0.12 -0.19 0.27 0.30 0.12 0.33 0.26 0.16
## R101_18 0.32 0.24 0.02 0.07 0.31 0.28 0.46 0.04 0.08
## R101_19 0.07 0.11 0.12 0.28 0.14 0.13 0.24 0.01 0.02
## R101_20 0.28 0.32 0.03 0.45 0.40 0.17 0.32 0.13 0.18
## R101_21 0.18 0.19 0.03 0.56 0.18 0.02 0.30 0.08 0.07
## R101_22 0.40 0.24 -0.21 0.17 0.39 0.19 0.15 0.35 0.67
## R101_23 0.01 0.06 0.03 0.09 -0.07 -0.12 0.07 -0.25 -0.03
## R101_24 -0.17 0.05 0.31 0.19 -0.12 -0.06 0.10 -0.22 -0.13
## R101_10 R101_11 R101_12 R101_13 R101_14 R101_15 R101_16 R101_17 R101_18
## R101_01 0.20 0.20 0.38 0.29 0.19 0.21 0.49 0.24 0.32
## R101_02 0.18 0.04 0.33 0.52 0.41 0.46 0.20 0.12 0.24
## R101_03 0.00 -0.12 -0.14 0.07 0.02 0.08 -0.05 -0.19 0.02
## R101_04 0.17 0.04 0.04 0.13 0.15 0.12 0.28 0.27 0.07
## R101_05 0.20 0.25 0.45 0.36 0.21 0.18 0.41 0.30 0.31
## R101_06 0.16 0.01 0.35 0.41 0.31 0.31 0.19 0.12 0.28
## R101_07 0.36 0.03 0.51 0.57 0.51 0.53 0.49 0.33 0.46
## R101_08 -0.03 0.76 0.28 0.16 0.05 0.06 0.23 0.26 0.04
## R101_09 0.17 0.39 0.17 0.17 0.07 0.08 0.21 0.16 0.08
## R101_10 1.00 -0.09 0.21 0.31 0.32 0.33 0.18 0.07 0.03
## R101_11 -0.09 1.00 0.19 0.08 -0.03 -0.09 0.11 0.23 0.08
## R101_12 0.21 0.19 1.00 0.42 0.23 0.28 0.33 0.22 0.28
## R101_13 0.31 0.08 0.42 1.00 0.50 0.58 0.35 0.29 0.37
## R101_14 0.32 -0.03 0.23 0.50 1.00 0.71 0.30 0.24 0.35
## R101_15 0.33 -0.09 0.28 0.58 0.71 1.00 0.30 0.31 0.39
## R101_16 0.18 0.11 0.33 0.35 0.30 0.30 1.00 0.54 0.22
## R101_17 0.07 0.23 0.22 0.29 0.24 0.31 0.54 1.00 0.34
## R101_18 0.03 0.08 0.28 0.37 0.35 0.39 0.22 0.34 1.00
## R101_19 0.05 0.04 0.09 0.36 0.17 0.31 0.22 0.31 0.41
## R101_20 0.20 0.18 0.19 0.35 0.36 0.29 0.42 0.44 0.37
## R101_21 0.25 0.10 0.16 0.28 0.34 0.31 0.32 0.40 0.38
## R101_22 0.26 0.29 0.26 0.15 0.08 0.09 0.21 0.18 0.16
## R101_23 0.12 -0.23 -0.12 0.15 0.25 0.21 0.04 0.11 0.12
## R101_24 0.08 -0.23 -0.16 0.13 0.20 0.25 0.04 0.13 0.10
## R101_19 R101_20 R101_21 R101_22 R101_23 R101_24
## R101_01 0.07 0.28 0.18 0.40 0.01 -0.17
## R101_02 0.11 0.32 0.19 0.24 0.06 0.05
## R101_03 0.12 0.03 0.03 -0.21 0.03 0.31
## R101_04 0.28 0.45 0.56 0.17 0.09 0.19
## R101_05 0.14 0.40 0.18 0.39 -0.07 -0.12
## R101_06 0.13 0.17 0.02 0.19 -0.12 -0.06
## R101_07 0.24 0.32 0.30 0.15 0.07 0.10
## R101_08 0.01 0.13 0.08 0.35 -0.25 -0.22
## R101_09 0.02 0.18 0.07 0.67 -0.03 -0.13
## R101_10 0.05 0.20 0.25 0.26 0.12 0.08
## R101_11 0.04 0.18 0.10 0.29 -0.23 -0.23
## R101_12 0.09 0.19 0.16 0.26 -0.12 -0.16
## R101_13 0.36 0.35 0.28 0.15 0.15 0.13
## R101_14 0.17 0.36 0.34 0.08 0.25 0.20
## R101_15 0.31 0.29 0.31 0.09 0.21 0.25
## R101_16 0.22 0.42 0.32 0.21 0.04 0.04
## R101_17 0.31 0.44 0.40 0.18 0.11 0.13
## R101_18 0.41 0.37 0.38 0.16 0.12 0.10
## R101_19 1.00 0.42 0.43 0.14 0.19 0.19
## R101_20 0.42 1.00 0.64 0.16 0.11 0.23
## R101_21 0.43 0.64 1.00 0.15 0.15 0.22
## R101_22 0.14 0.16 0.15 1.00 0.08 -0.11
## R101_23 0.19 0.11 0.15 0.08 1.00 0.45
## R101_24 0.19 0.23 0.22 -0.11 0.45 1.00
# Und hier noch zur Freude aller eine grafische Darstellung der Korrelationen:
items |>
corrr::correlate() |>
corrr::rplot()
## Correlation computed with
## • Method: 'pearson'
## • Missing treated using: 'pairwise.complete.obs'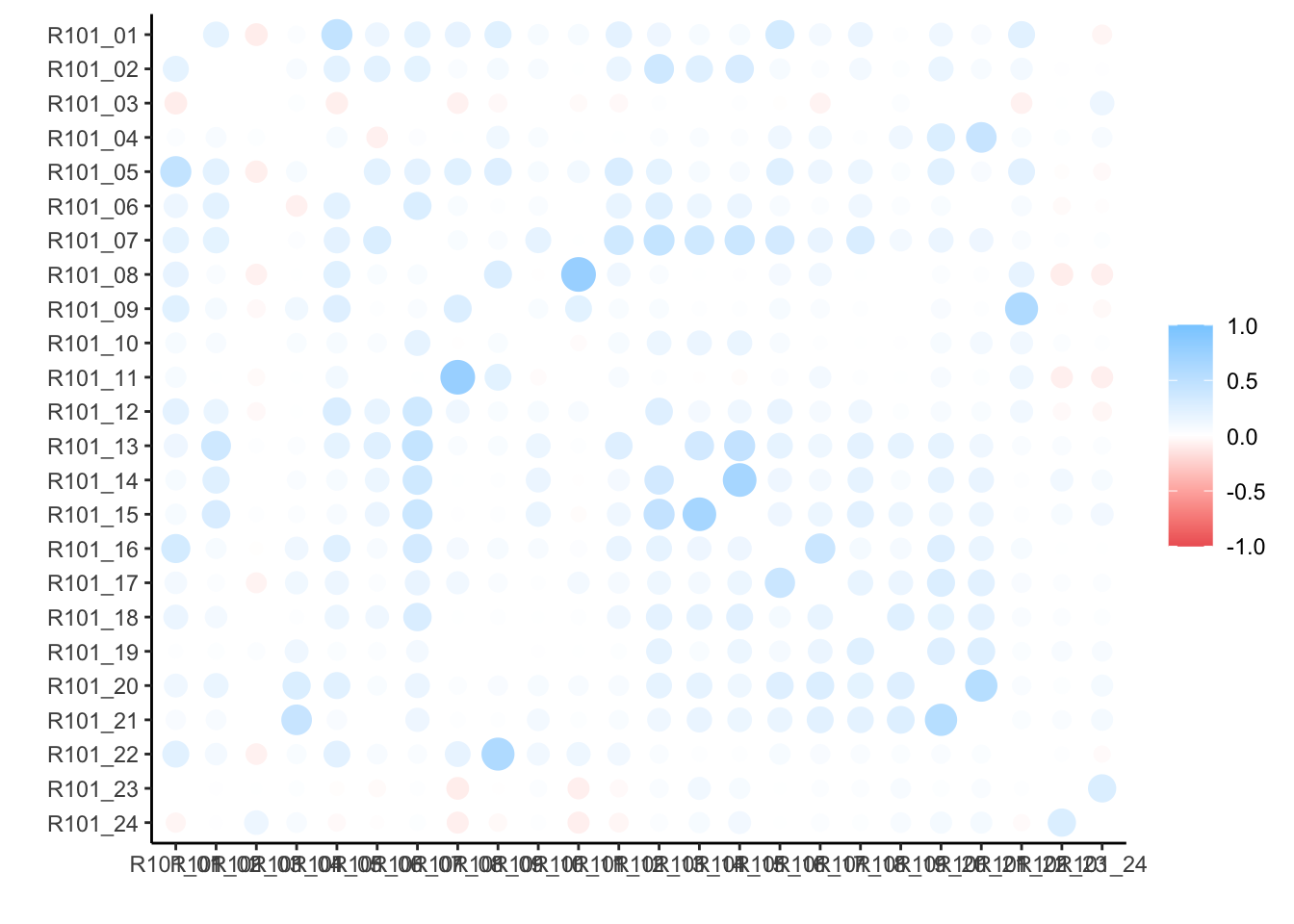
3.2 Bartlett-Test
Unterscheiden sich die Korrelationen aller Variablen mit allen anderen Variablen von 0? Etwas technischer: Hebt sich die tatsächliche Korrelationsmatrix (mit den 1 in der Diagonale und Werten daneben für die Kombis) von einer Matrix ab, die nur Nullen neben der Diagonalen hat?
R-Code
items |>
cor() |>
psych::cortest.bartlett(nrow(DATEN))
## $chisq
## [1] 1772.52
##
## $p.value
## [1] 1.953148e-216
##
## $df
## [1] 276Volle Lotte!
3.3 KMO-Test
Der KMO fragt im Grunde, wie viel eine Variable mit irgendwelchen übrigen Variablen gemeinsam hat. Wenn der Wert nahe 1 ist, ist eine Variable für eine Faktorenanalyse mit den übrigen Variablen geeignet. Den MSA (Measure of Sampling Adequacy) gibt es für jedes item, aber auch für als Gesamtmass für alle Variablen. Unser Wert hier von .78 ist schon ganz gut.
## Kaiser-Meyer-Olkin factor adequacy
## Call: psych::KMO(r = items)
## Overall MSA = 0.78
## MSA for each item =
## R101_01 R101_02 R101_03 R101_04 R101_05 R101_06 R101_07 R101_08 R101_09 R101_10
## 0.85 0.83 0.55 0.67 0.87 0.77 0.88 0.69 0.72 0.73
## R101_11 R101_12 R101_13 R101_14 R101_15 R101_16 R101_17 R101_18 R101_19 R101_20
## 0.62 0.88 0.90 0.81 0.80 0.79 0.80 0.76 0.75 0.83
## R101_21 R101_22 R101_23 R101_24
## 0.80 0.71 0.62 0.72
## Kaiser-Meyer-Olkin factor adequacy
## Call: psych::KMO(r = items)
## Overall MSA = 0.78
## MSA for each item =
## R101_01 R101_02 R101_03 R101_04 R101_05 R101_06 R101_07 R101_08 R101_09 R101_10
## 0.85 0.83 0.55 0.67 0.87 0.77 0.88 0.69 0.72 0.73
## R101_11 R101_12 R101_13 R101_14 R101_15 R101_16 R101_17 R101_18 R101_19 R101_20
## 0.62 0.88 0.90 0.81 0.80 0.79 0.80 0.76 0.75 0.83
## R101_21 R101_22 R101_23 R101_24
## 0.80 0.71 0.62 0.723.4 Parallelanalyse
Mit der Parallelanalyse kann festgestellt werden, wie viele Faktoren aus einem item-set extrahiert werden können bzw. sollten. Ein Orientierungspunkt ist der Eigenwert, also der Wert der angibt, ob ein Faktor mehr Varianz (>1) oder weniger (<1) als eine einzelne Variable auf sich vereint. Wenn der Eigenwert fast gleich 1 ist, kann man sagen, dass es schon noch sinnvoll ist den aufzunehmen, aber auch sagen, dass in dem Fall keine Dimensionsreduktion mehr stattfindet und der Faktor nicht mehr aufgenommen wird. Generell empfehle ich in Zweifelsfällen, die Analysen mal mit dem einen Faktor mehr und einmal mit dem Faktor weniger durchzuführen.
R-Code
items |>
psych::fa.parallel(# fa = "fa" #
)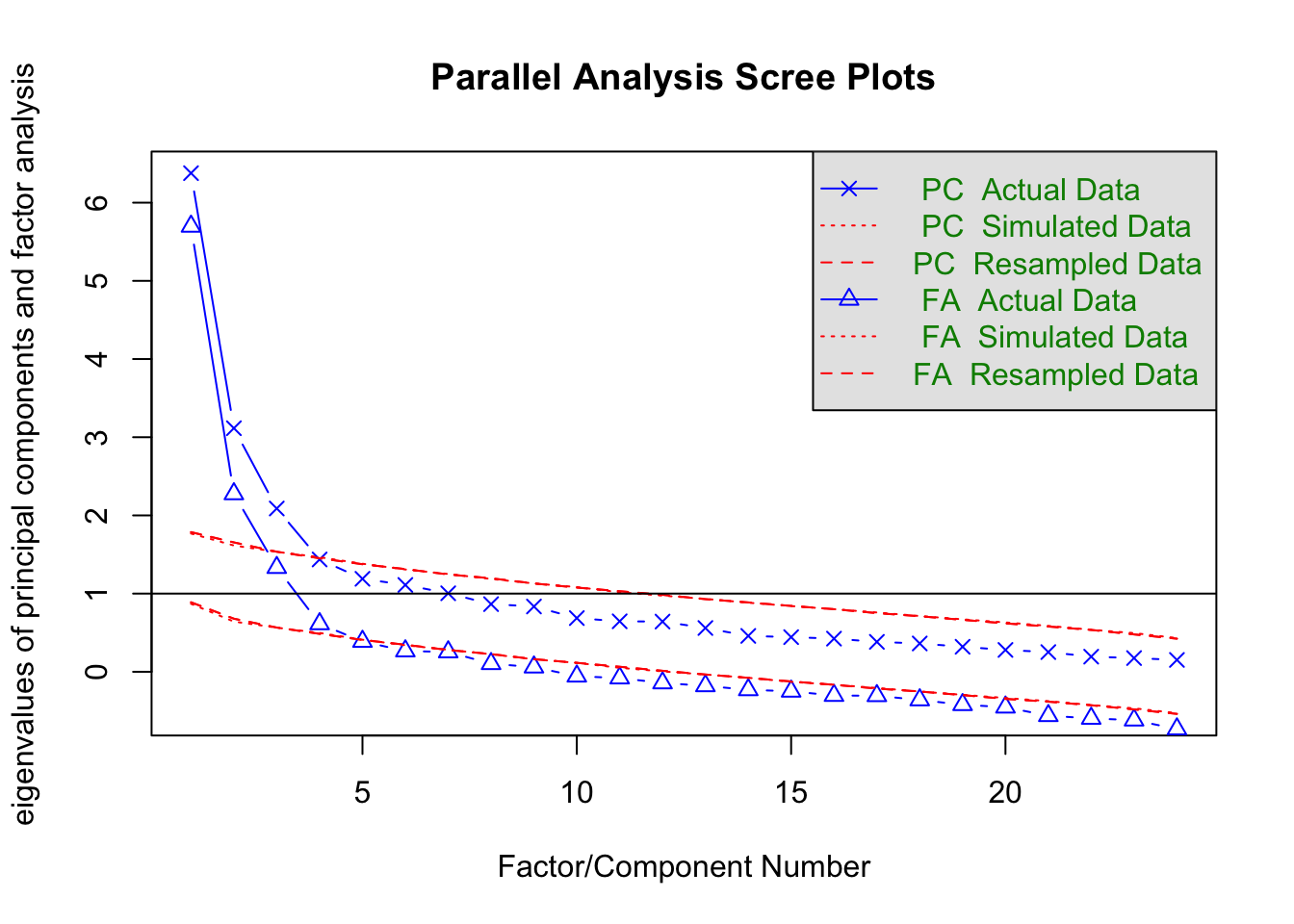
## Parallel analysis suggests that the number of factors = 4 and the number of components = 3Wir gehen erstmal von 3 Hauptkomponten aus und probieren aber auch 4.
3.5 Die Faktorenanalyse
Einfach
Direkt einfach nur die Faktorenanalyse.
items |>
psych::fa(nfactors = 4,
rotate = "varimax")
## Factor Analysis using method = minres
## Call: psych::fa(r = items, nfactors = 4, rotate = "varimax")
## Standardized loadings (pattern matrix) based upon correlation matrix
## MR1 MR3 MR2 MR4 h2 u2 com
## R101_01 0.43 0.16 0.33 0.38 0.46 0.54 3.2
## R101_02 0.55 0.11 -0.02 0.24 0.37 0.63 1.5
## R101_03 -0.02 0.06 -0.31 -0.16 0.12 0.88 1.6
## R101_04 -0.08 0.59 -0.15 0.31 0.48 0.52 1.7
## R101_05 0.45 0.22 0.38 0.37 0.52 0.48 3.4
## R101_06 0.63 -0.09 0.17 -0.01 0.44 0.56 1.2
## R101_07 0.74 0.24 0.03 0.04 0.61 0.39 1.2
## R101_08 0.12 0.17 0.69 0.25 0.59 0.41 1.5
## R101_09 0.08 0.10 0.27 0.78 0.69 0.31 1.3
## R101_10 0.34 0.08 -0.20 0.29 0.24 0.76 2.7
## R101_11 -0.05 0.23 0.64 0.18 0.50 0.50 1.5
## R101_12 0.54 0.09 0.31 0.11 0.41 0.59 1.8
## R101_13 0.70 0.26 -0.05 0.09 0.56 0.44 1.3
## R101_14 0.62 0.25 -0.24 0.07 0.51 0.49 1.7
## R101_15 0.69 0.25 -0.26 0.04 0.60 0.40 1.6
## R101_16 0.38 0.43 0.17 0.14 0.38 0.62 2.6
## R101_17 0.24 0.57 0.18 0.04 0.42 0.58 1.6
## R101_18 0.45 0.37 0.03 -0.04 0.34 0.66 2.0
## R101_19 0.20 0.52 -0.10 -0.03 0.32 0.68 1.4
## R101_20 0.26 0.71 0.00 0.12 0.59 0.41 1.3
## R101_21 0.15 0.76 -0.12 0.08 0.61 0.39 1.2
## R101_22 0.16 0.10 0.21 0.70 0.57 0.43 1.3
## R101_23 0.07 0.18 -0.46 0.11 0.26 0.74 1.5
## R101_24 0.04 0.29 -0.52 -0.05 0.36 0.64 1.6
##
## MR1 MR3 MR2 MR4
## SS loadings 3.98 2.91 2.25 1.83
## Proportion Var 0.17 0.12 0.09 0.08
## Cumulative Var 0.17 0.29 0.38 0.46
## Proportion Explained 0.36 0.27 0.21 0.17
## Cumulative Proportion 0.36 0.63 0.83 1.00
##
## Mean item complexity = 1.7
## Test of the hypothesis that 4 factors are sufficient.
##
## df null model = 276 with the objective function = 11.28 with Chi Square = 1761.24
## df of the model are 186 and the objective function was 2.86
##
## The root mean square of the residuals (RMSR) is 0.05
## The df corrected root mean square of the residuals is 0.07
##
## The harmonic n.obs is 166 with the empirical chi square 262.91 with prob < 0.00018
## The total n.obs was 166 with Likelihood Chi Square = 438.34 with prob < 2e-22
##
## Tucker Lewis Index of factoring reliability = 0.743
## RMSEA index = 0.09 and the 90 % confidence intervals are 0.08 0.102
## BIC = -512.49
## Fit based upon off diagonal values = 0.96
## Measures of factor score adequacy
## MR1 MR3 MR2 MR4
## Correlation of (regression) scores with factors 0.93 0.90 0.89 0.87
## Multiple R square of scores with factors 0.86 0.81 0.78 0.75
## Minimum correlation of possible factor scores 0.72 0.61 0.57 0.50Die Lösung speichern (wie beim lm-Modell)
Erstmal die (unrotiert) Faktorenanalyse in m.ml.u speichern und dann ausgeben mit print():
m.ml.u <- items |>
psych::fa(
nfactors=4,
n.obs = nrow(DATEN),
SMC=TRUE,
rotate="none",
max.iter=100
)
print(m.ml.u)
## Factor Analysis using method = minres
## Call: psych::fa(r = items, nfactors = 4, n.obs = nrow(DATEN), rotate = "none",
## SMC = TRUE, max.iter = 100)
## Standardized loadings (pattern matrix) based upon correlation matrix
## MR1 MR2 MR3 MR4 h2 u2 com
## R101_01 0.58 -0.33 -0.08 0.08 0.46 0.54 1.7
## R101_02 0.55 0.04 -0.22 0.15 0.37 0.63 1.5
## R101_03 -0.08 0.34 0.03 0.01 0.12 0.88 1.1
## R101_04 0.35 0.14 0.56 0.15 0.48 0.52 2.0
## R101_05 0.63 -0.34 -0.05 0.02 0.52 0.48 1.6
## R101_06 0.45 -0.06 -0.48 -0.09 0.44 0.56 2.1
## R101_07 0.71 0.14 -0.29 -0.08 0.61 0.39 1.5
## R101_08 0.38 -0.63 0.10 -0.20 0.59 0.41 1.9
## R101_09 0.42 -0.52 0.21 0.45 0.69 0.31 3.3
## R101_10 0.37 0.12 -0.09 0.30 0.24 0.76 2.3
## R101_11 0.25 -0.57 0.23 -0.24 0.50 0.50 2.2
## R101_12 0.53 -0.20 -0.27 -0.11 0.41 0.59 1.9
## R101_13 0.68 0.19 -0.24 0.00 0.56 0.44 1.4
## R101_14 0.59 0.34 -0.20 0.08 0.51 0.49 1.9
## R101_15 0.62 0.39 -0.25 0.06 0.60 0.40 2.1
## R101_16 0.60 -0.03 0.09 -0.12 0.38 0.62 1.1
## R101_17 0.53 0.02 0.26 -0.25 0.42 0.58 1.9
## R101_18 0.53 0.16 -0.03 -0.18 0.34 0.66 1.4
## R101_19 0.41 0.27 0.24 -0.15 0.32 0.68 2.8
## R101_20 0.63 0.18 0.37 -0.14 0.59 0.41 1.9
## R101_21 0.54 0.29 0.47 -0.12 0.61 0.39 2.6
## R101_22 0.44 -0.42 0.14 0.42 0.57 0.43 3.2
## R101_23 0.12 0.41 0.12 0.27 0.26 0.74 2.1
## R101_24 0.10 0.55 0.18 0.12 0.36 0.64 1.4
##
## MR1 MR2 MR3 MR4
## SS loadings 5.87 2.60 1.59 0.91
## Proportion Var 0.24 0.11 0.07 0.04
## Cumulative Var 0.24 0.35 0.42 0.46
## Proportion Explained 0.54 0.24 0.14 0.08
## Cumulative Proportion 0.54 0.77 0.92 1.00
##
## Mean item complexity = 2
## Test of the hypothesis that 4 factors are sufficient.
##
## df null model = 276 with the objective function = 11.28 with Chi Square = 1761.24
## df of the model are 186 and the objective function was 2.86
##
## The root mean square of the residuals (RMSR) is 0.05
## The df corrected root mean square of the residuals is 0.07
##
## The harmonic n.obs is 166 with the empirical chi square 262.91 with prob < 0.00018
## The total n.obs was 166 with Likelihood Chi Square = 438.34 with prob < 2e-22
##
## Tucker Lewis Index of factoring reliability = 0.743
## RMSEA index = 0.09 and the 90 % confidence intervals are 0.08 0.102
## BIC = -512.49
## Fit based upon off diagonal values = 0.96
## Measures of factor score adequacy
## MR1 MR2 MR3 MR4
## Correlation of (regression) scores with factors 0.96 0.92 0.88 0.81
## Multiple R square of scores with factors 0.93 0.85 0.77 0.66
## Minimum correlation of possible factor scores 0.85 0.69 0.54 0.32Nur die Loadings
Hier mal nur die Faktorladungen (nur für Ladungen über .4):
print(m.ml.u$loadings, cutoff=.4)
##
## Loadings:
## MR1 MR2 MR3 MR4
## R101_01 0.583
## R101_02 0.548
## R101_03
## R101_04 0.556
## R101_05 0.635
## R101_06 0.445 -0.478
## R101_07 0.707
## R101_08 -0.631
## R101_09 0.420 -0.518 0.453
## R101_10
## R101_11 -0.567
## R101_12 0.534
## R101_13 0.684
## R101_14 0.586
## R101_15 0.621
## R101_16 0.596
## R101_17 0.535
## R101_18 0.532
## R101_19 0.406
## R101_20 0.632
## R101_21 0.545 0.468
## R101_22 0.443 -0.419 0.420
## R101_23 0.407
## R101_24 0.547
##
## MR1 MR2 MR3 MR4
## SS loadings 5.874 2.597 1.588 0.906
## Proportion Var 0.245 0.108 0.066 0.038
## Cumulative Var 0.245 0.353 0.419 0.4573.6 Rotierte Faktorenlösung
Die initiale Faktorextraktion geht in der Regel schrittweise vor, indem der erste Faktor das Maximale an Varianz versucht zu erfassen. Der zweite Faktor kann noch den Rest (praktisch die Residuen der der ersten Faktorgeraden) abbilden. Der dritte Faktor den dann noch übrigen Rest und so weiter. Wenn das gemacht ist, kann man schauen, wie viele Faktoren noch ausreichend Varianz aufklären (Eigenwerte >1). Dann haben wir aber das Problem, dass die aufgeklärte Varianz nicht gut auf die Faktoren verteilt ist. Aber wir können unsere extrahierten Faktoren (sagen wir 4) noch gut in dem 4-dimensionalen Raum drehen und anpassen, so dass jeder Faktor möglichst gleich viel Varianzproportionen abbildet (VARIMAX-Methode), während die Faktoren unkorreliert bleiben müssen (orthogonal). Etwas realistischer ist allerdings die Methode, bei der jeder Faktor maximale Varianzproportionen (promax) auf sich vereint und die Faktoren leicht miteinander korrelieren dürfen (oblimin):
R-Code
m.ml.r <- psych::fa(items,
nfactors=4,
n.obs = nrow(items),
SMC=TRUE,
fm="ml",
# rotate="varimax",
rotate="promax",
max.iter=100
)
## Loading required namespace: GPArotation
print(m.ml.r)
## Factor Analysis using method = ml
## Call: psych::fa(r = items, nfactors = 4, n.obs = nrow(items), rotate = "promax",
## SMC = TRUE, max.iter = 100, fm = "ml")
## Standardized loadings (pattern matrix) based upon correlation matrix
## ML2 ML3 ML4 ML1 h2 u2 com
## R101_01 0.21 0.08 0.66 -0.08 0.55 0.451 1.3
## R101_02 0.55 -0.02 0.15 -0.03 0.36 0.640 1.2
## R101_03 0.08 0.07 -0.41 0.05 0.15 0.853 1.2
## R101_04 -0.35 0.82 0.21 -0.10 0.50 0.500 1.5
## R101_05 0.20 0.14 0.68 -0.05 0.62 0.383 1.3
## R101_06 0.67 -0.35 0.18 -0.05 0.40 0.596 1.7
## R101_07 0.74 -0.02 0.08 -0.01 0.57 0.425 1.0
## R101_08 0.12 -0.01 0.21 0.68 0.67 0.325 1.2
## R101_09 -0.05 0.17 0.51 0.17 0.38 0.617 1.5
## R101_10 0.30 0.10 0.13 -0.16 0.18 0.819 2.1
## R101_11 -0.04 0.12 -0.07 1.03 1.00 0.005 1.0
## R101_12 0.48 -0.11 0.30 0.06 0.38 0.618 1.9
## R101_13 0.77 0.00 -0.06 0.10 0.57 0.434 1.0
## R101_14 0.78 0.04 -0.26 0.07 0.57 0.425 1.3
## R101_15 0.88 -0.02 -0.29 0.03 0.68 0.320 1.2
## R101_16 0.21 0.33 0.36 -0.06 0.39 0.607 2.7
## R101_17 0.13 0.44 0.10 0.16 0.34 0.663 1.6
## R101_18 0.42 0.20 -0.01 0.07 0.31 0.688 1.5
## R101_19 0.13 0.47 -0.12 0.06 0.30 0.703 1.3
## R101_20 0.04 0.73 0.11 0.08 0.60 0.400 1.1
## R101_21 -0.05 0.83 -0.01 0.04 0.64 0.357 1.0
## R101_22 -0.01 0.16 0.52 0.06 0.34 0.658 1.2
## R101_23 0.11 0.22 -0.19 -0.17 0.16 0.836 3.4
## R101_24 0.11 0.32 -0.38 -0.09 0.30 0.700 2.3
##
## ML2 ML3 ML4 ML1
## SS loadings 4.03 2.76 2.45 1.74
## Proportion Var 0.17 0.12 0.10 0.07
## Cumulative Var 0.17 0.28 0.39 0.46
## Proportion Explained 0.37 0.25 0.22 0.16
## Cumulative Proportion 0.37 0.62 0.84 1.00
##
## With factor correlations of
## ML2 ML3 ML4 ML1
## ML2 1.00 0.55 0.30 0.00
## ML3 0.55 1.00 0.06 -0.03
## ML4 0.30 0.06 1.00 0.48
## ML1 0.00 -0.03 0.48 1.00
##
## Mean item complexity = 1.5
## Test of the hypothesis that 4 factors are sufficient.
##
## df null model = 276 with the objective function = 11.28 with Chi Square = 1761.24
## df of the model are 186 and the objective function was 2.66
##
## The root mean square of the residuals (RMSR) is 0.06
## The df corrected root mean square of the residuals is 0.07
##
## The harmonic n.obs is 166 with the empirical chi square 299.5 with prob < 2.5e-07
## The total n.obs was 166 with Likelihood Chi Square = 408.45 with prob < 1e-18
##
## Tucker Lewis Index of factoring reliability = 0.773
## RMSEA index = 0.085 and the 90 % confidence intervals are 0.074 0.096
## BIC = -542.38
## Fit based upon off diagonal values = 0.96
## Measures of factor score adequacy
## ML2 ML3 ML4 ML1
## Correlation of (regression) scores with factors 0.95 0.93 0.91 1.00
## Multiple R square of scores with factors 0.90 0.86 0.83 0.99
## Minimum correlation of possible factor scores 0.81 0.72 0.66 0.98Nur Ladungen > .3 und sortiert
Jetzt schauen wir mal die Faktorenladungen an und unterdrücken in der Ausgabe alle Werte, die kleiner gleich .3 sind und lassen nach der Grösse der Faktorladungen sortieren:
psych::print.psych(m.ml.r, cut=0.3, sort=T)
## Factor Analysis using method = ml
## Call: psych::fa(r = items, nfactors = 4, n.obs = nrow(items), rotate = "promax",
## SMC = TRUE, max.iter = 100, fm = "ml")
## Standardized loadings (pattern matrix) based upon correlation matrix
## item ML2 ML3 ML4 ML1 h2 u2 com
## R101_15 15 0.88 0.68 0.320 1.2
## R101_14 14 0.78 0.57 0.425 1.3
## R101_13 13 0.77 0.57 0.434 1.0
## R101_07 7 0.74 0.57 0.425 1.0
## R101_06 6 0.67 -0.35 0.40 0.596 1.7
## R101_02 2 0.55 0.36 0.640 1.2
## R101_12 12 0.48 0.30 0.38 0.618 1.9
## R101_18 18 0.42 0.31 0.688 1.5
## R101_10 10 0.30 0.18 0.819 2.1
## R101_21 21 0.83 0.64 0.357 1.0
## R101_04 4 -0.35 0.82 0.50 0.500 1.5
## R101_20 20 0.73 0.60 0.400 1.1
## R101_19 19 0.47 0.30 0.703 1.3
## R101_17 17 0.44 0.34 0.663 1.6
## R101_23 23 0.16 0.836 3.4
## R101_05 5 0.68 0.62 0.383 1.3
## R101_01 1 0.66 0.55 0.451 1.3
## R101_22 22 0.52 0.34 0.658 1.2
## R101_09 9 0.51 0.38 0.617 1.5
## R101_03 3 -0.41 0.15 0.853 1.2
## R101_24 24 0.32 -0.38 0.30 0.700 2.3
## R101_16 16 0.33 0.36 0.39 0.607 2.7
## R101_11 11 1.03 1.00 0.005 1.0
## R101_08 8 0.68 0.67 0.325 1.2
##
## ML2 ML3 ML4 ML1
## SS loadings 4.03 2.76 2.45 1.74
## Proportion Var 0.17 0.12 0.10 0.07
## Cumulative Var 0.17 0.28 0.39 0.46
## Proportion Explained 0.37 0.25 0.22 0.16
## Cumulative Proportion 0.37 0.62 0.84 1.00
##
## With factor correlations of
## ML2 ML3 ML4 ML1
## ML2 1.00 0.55 0.30 0.00
## ML3 0.55 1.00 0.06 -0.03
## ML4 0.30 0.06 1.00 0.48
## ML1 0.00 -0.03 0.48 1.00
##
## Mean item complexity = 1.5
## Test of the hypothesis that 4 factors are sufficient.
##
## df null model = 276 with the objective function = 11.28 with Chi Square = 1761.24
## df of the model are 186 and the objective function was 2.66
##
## The root mean square of the residuals (RMSR) is 0.06
## The df corrected root mean square of the residuals is 0.07
##
## The harmonic n.obs is 166 with the empirical chi square 299.5 with prob < 2.5e-07
## The total n.obs was 166 with Likelihood Chi Square = 408.45 with prob < 1e-18
##
## Tucker Lewis Index of factoring reliability = 0.773
## RMSEA index = 0.085 and the 90 % confidence intervals are 0.074 0.096
## BIC = -542.38
## Fit based upon off diagonal values = 0.96
## Measures of factor score adequacy
## ML2 ML3 ML4 ML1
## Correlation of (regression) scores with factors 0.95 0.93 0.91 1.00
## Multiple R square of scores with factors 0.90 0.86 0.83 0.99
## Minimum correlation of possible factor scores 0.81 0.72 0.66 0.98Ein FA-Diagramm
Man kann auch Diagramme rauslassen, die allerdings noch etwas Nacharbeit brauchen würden, bis sie gut lesbar sind. Dazu sollte man im Fall die Vignette von psych konsultieren.
m.ml.r |>
psych::fa.diagram()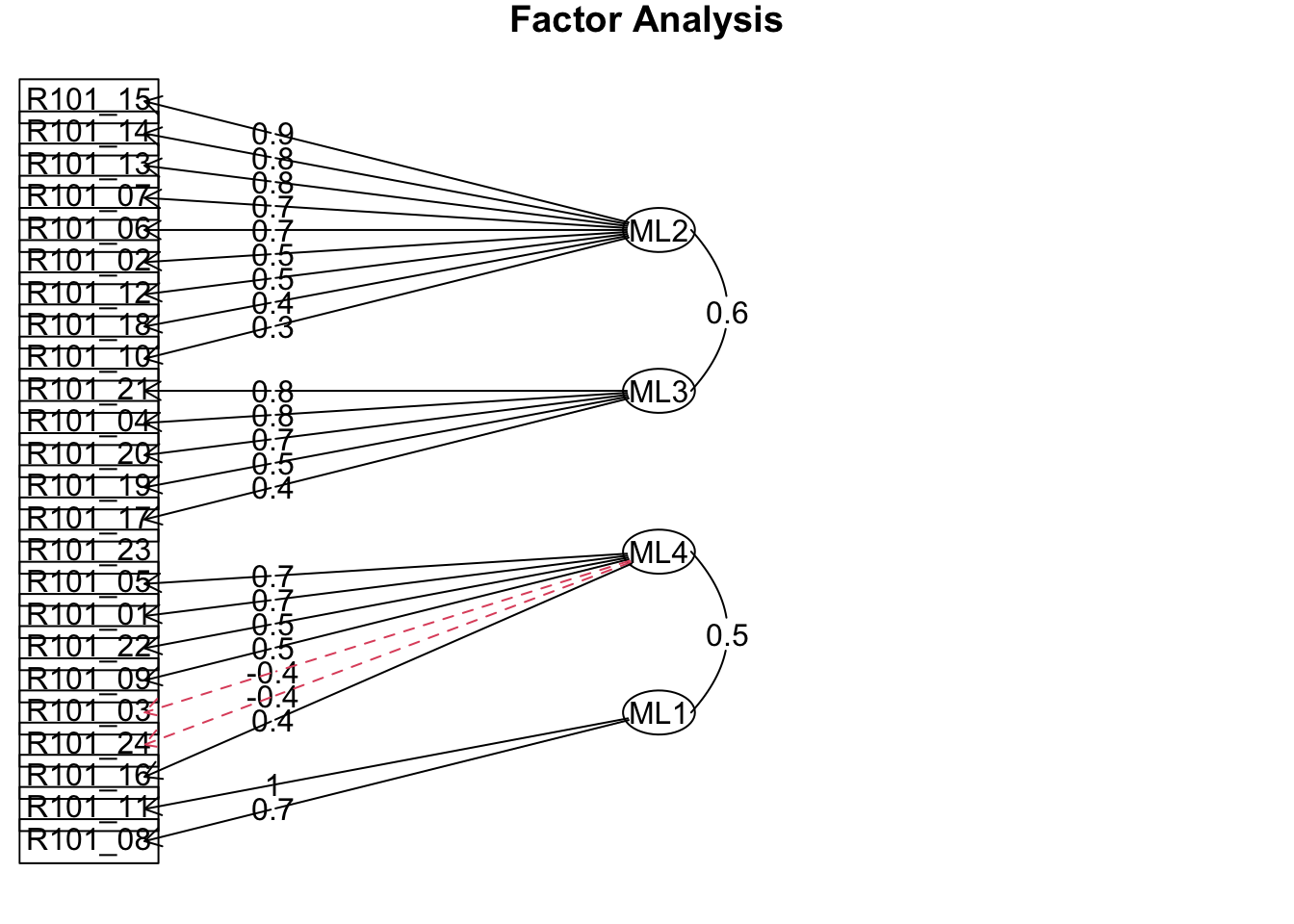
3.7 Führen Sie eine FA mit Oblimin-Rotation durch
m.ml.oblimin <- psych::fa(items,
nfactors=4,
n.obs = nrow(items),
SMC=TRUE,
fm="ml",
#rotate="varimax",
rotate="promax",
max.iter=100
)
psych::print.psych(m.ml.oblimin, cut=0.3, sort=T)
## Factor Analysis using method = ml
## Call: psych::fa(r = items, nfactors = 4, n.obs = nrow(items), rotate = "promax",
## SMC = TRUE, max.iter = 100, fm = "ml")
## Standardized loadings (pattern matrix) based upon correlation matrix
## item ML2 ML3 ML4 ML1 h2 u2 com
## R101_15 15 0.88 0.68 0.320 1.2
## R101_14 14 0.78 0.57 0.425 1.3
## R101_13 13 0.77 0.57 0.434 1.0
## R101_07 7 0.74 0.57 0.425 1.0
## R101_06 6 0.67 -0.35 0.40 0.596 1.7
## R101_02 2 0.55 0.36 0.640 1.2
## R101_12 12 0.48 0.30 0.38 0.618 1.9
## R101_18 18 0.42 0.31 0.688 1.5
## R101_10 10 0.30 0.18 0.819 2.1
## R101_21 21 0.83 0.64 0.357 1.0
## R101_04 4 -0.35 0.82 0.50 0.500 1.5
## R101_20 20 0.73 0.60 0.400 1.1
## R101_19 19 0.47 0.30 0.703 1.3
## R101_17 17 0.44 0.34 0.663 1.6
## R101_23 23 0.16 0.836 3.4
## R101_05 5 0.68 0.62 0.383 1.3
## R101_01 1 0.66 0.55 0.451 1.3
## R101_22 22 0.52 0.34 0.658 1.2
## R101_09 9 0.51 0.38 0.617 1.5
## R101_03 3 -0.41 0.15 0.853 1.2
## R101_24 24 0.32 -0.38 0.30 0.700 2.3
## R101_16 16 0.33 0.36 0.39 0.607 2.7
## R101_11 11 1.03 1.00 0.005 1.0
## R101_08 8 0.68 0.67 0.325 1.2
##
## ML2 ML3 ML4 ML1
## SS loadings 4.03 2.76 2.45 1.74
## Proportion Var 0.17 0.12 0.10 0.07
## Cumulative Var 0.17 0.28 0.39 0.46
## Proportion Explained 0.37 0.25 0.22 0.16
## Cumulative Proportion 0.37 0.62 0.84 1.00
##
## With factor correlations of
## ML2 ML3 ML4 ML1
## ML2 1.00 0.55 0.30 0.00
## ML3 0.55 1.00 0.06 -0.03
## ML4 0.30 0.06 1.00 0.48
## ML1 0.00 -0.03 0.48 1.00
##
## Mean item complexity = 1.5
## Test of the hypothesis that 4 factors are sufficient.
##
## df null model = 276 with the objective function = 11.28 with Chi Square = 1761.24
## df of the model are 186 and the objective function was 2.66
##
## The root mean square of the residuals (RMSR) is 0.06
## The df corrected root mean square of the residuals is 0.07
##
## The harmonic n.obs is 166 with the empirical chi square 299.5 with prob < 2.5e-07
## The total n.obs was 166 with Likelihood Chi Square = 408.45 with prob < 1e-18
##
## Tucker Lewis Index of factoring reliability = 0.773
## RMSEA index = 0.085 and the 90 % confidence intervals are 0.074 0.096
## BIC = -542.38
## Fit based upon off diagonal values = 0.96
## Measures of factor score adequacy
## ML2 ML3 ML4 ML1
## Correlation of (regression) scores with factors 0.95 0.93 0.91 1.00
## Multiple R square of scores with factors 0.90 0.86 0.83 0.99
## Minimum correlation of possible factor scores 0.81 0.72 0.66 0.98Faktoren in die Daten speichern
Das Speichern ist nicht so einfach, weil die Faktoren der Faktoranalyse nur als Vectoren ausgegeben werden und dann nur für die Fälle, die keine fehlenden Werte in den Variablen der Faktorenanlyse haben. Darum muss man (wenn man fehlende Werte hat) erstmal einen Hilfsdatensatz erstellen mit den Fall-IDs (bei uns die CASES). Dann bindet man die neuen Faktor$scores mit column bind cbind() zusammen und kann das dann mit left_join an den ursprünglichen Datensatz matchen.
DATEN |> sjmisc::frq(R101_01:R101_24)
## RAQ: Statistik bringt mich zum Weinen. (R101_01) <integer>
## # total N=167 valid N=167 mean=2.95 sd=1.34
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 29 | 17.37 | 17.37 | 17.37
## 2 | 2 | 42 | 25.15 | 25.15 | 42.51
## 3 | 3 | 30 | 17.96 | 17.96 | 60.48
## 4 | 4 | 41 | 24.55 | 24.55 | 85.03
## 5 | 5 trifft voll und ganz zu | 25 | 14.97 | 14.97 | 100.00
## <NA> | <NA> | 0 | 0.00 | <NA> | <NA>
##
## RAQ: Meine Freunde werden denken, ich sei dumm, weil ich nicht mit R umgehen kann. (R101_02) <integer>
## # total N=167 valid N=166 mean=1.83 sd=1.09
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 86 | 51.50 | 51.81 | 51.81
## 2 | 2 | 45 | 26.95 | 27.11 | 78.92
## 3 | 3 | 17 | 10.18 | 10.24 | 89.16
## 4 | 4 | 13 | 7.78 | 7.83 | 96.99
## 5 | 5 trifft voll und ganz zu | 5 | 2.99 | 3.01 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Standardabweichungen begeistern mich. (R101_03) <integer>
## # total N=167 valid N=166 mean=1.94 sd=0.93
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 63 | 37.72 | 37.95 | 37.95
## 2 | 2 | 62 | 37.13 | 37.35 | 75.30
## 3 | 3 | 31 | 18.56 | 18.67 | 93.98
## 4 | 4 | 8 | 4.79 | 4.82 | 98.80
## 5 | 5 trifft voll und ganz zu | 2 | 1.20 | 1.20 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich träume davon, dass Pearson mich mit Korrelationskoeffizienten angreift. (R101_04) <integer>
## # total N=167 valid N=166 mean=1.83 sd=1.27
##
## Value | Label | N | Raw % | Valid % | Cum. %
## --------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 102 | 61.08 | 61.45 | 61.45
## 2 | 2 | 27 | 16.17 | 16.27 | 77.71
## 3 | 3 | 14 | 8.38 | 8.43 | 86.14
## 4 | 4 | 10 | 5.99 | 6.02 | 92.17
## 5 | 5 trifft voll und ganz zu | 13 | 7.78 | 7.83 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich verstehe Statistik nicht. (R101_05) <integer>
## # total N=167 valid N=166 mean=2.81 sd=1.14
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 21 | 12.57 | 12.65 | 12.65
## 2 | 2 | 48 | 28.74 | 28.92 | 41.57
## 3 | 3 | 52 | 31.14 | 31.33 | 72.89
## 4 | 4 | 31 | 18.56 | 18.67 | 91.57
## 5 | 5 trifft voll und ganz zu | 14 | 8.38 | 8.43 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich habe wenig Erfahrung mit Computern. (R101_06) <integer>
## # total N=167 valid N=166 mean=2.63 sd=1.16
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 33 | 19.76 | 19.88 | 19.88
## 2 | 2 | 47 | 28.14 | 28.31 | 48.19
## 3 | 3 | 41 | 24.55 | 24.70 | 72.89
## 4 | 4 | 38 | 22.75 | 22.89 | 95.78
## 5 | 5 trifft voll und ganz zu | 7 | 4.19 | 4.22 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Alle Computer hassen mich. (R101_07) <integer>
## # total N=167 valid N=167 mean=1.94 sd=1.20
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 87 | 52.10 | 52.10 | 52.10
## 2 | 2 | 31 | 18.56 | 18.56 | 70.66
## 3 | 3 | 31 | 18.56 | 18.56 | 89.22
## 4 | 4 | 8 | 4.79 | 4.79 | 94.01
## 5 | 5 trifft voll und ganz zu | 10 | 5.99 | 5.99 | 100.00
## <NA> | <NA> | 0 | 0.00 | <NA> | <NA>
##
## RAQ: Ich war noch nie gut in Mathe. (R101_08) <integer>
## # total N=167 valid N=166 mean=2.66 sd=1.22
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 32 | 19.16 | 19.28 | 19.28
## 2 | 2 | 51 | 30.54 | 30.72 | 50.00
## 3 | 3 | 40 | 23.95 | 24.10 | 74.10
## 4 | 4 | 28 | 16.77 | 16.87 | 90.96
## 5 | 5 trifft voll und ganz zu | 15 | 8.98 | 9.04 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Meine Freunde sind besser in Statistik als ich. (R101_09) <integer>
## # total N=167 valid N=166 mean=2.95 sd=1.07
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 12 | 7.19 | 7.23 | 7.23
## 2 | 2 | 46 | 27.54 | 27.71 | 34.94
## 3 | 3 | 62 | 37.13 | 37.35 | 72.29
## 4 | 4 | 30 | 17.96 | 18.07 | 90.36
## 5 | 5 trifft voll und ganz zu | 16 | 9.58 | 9.64 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Computer sind nur zum Spielen nützlich. (R101_10) <integer>
## # total N=167 valid N=166 mean=1.65 sd=0.98
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 98 | 58.68 | 59.04 | 59.04
## 2 | 2 | 43 | 25.75 | 25.90 | 84.94
## 3 | 3 | 16 | 9.58 | 9.64 | 94.58
## 4 | 4 | 3 | 1.80 | 1.81 | 96.39
## 5 | 5 trifft voll und ganz zu | 6 | 3.59 | 3.61 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich war in der Schule schlecht in Mathematik. (R101_11) <integer>
## # total N=167 valid N=167 mean=2.84 sd=1.28
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 32 | 19.16 | 19.16 | 19.16
## 2 | 2 | 36 | 21.56 | 21.56 | 40.72
## 3 | 3 | 45 | 26.95 | 26.95 | 67.66
## 4 | 4 | 35 | 20.96 | 20.96 | 88.62
## 5 | 5 trifft voll und ganz zu | 19 | 11.38 | 11.38 | 100.00
## <NA> | <NA> | 0 | 0.00 | <NA> | <NA>
##
## RAQ: Leute versuchen dir zu sagen, dass R die Statistik leichter verständlich macht, aber das stimmt nicht. (R101_12) <integer>
## # total N=167 valid N=166 mean=3.00 sd=1.25
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 24 | 14.37 | 14.46 | 14.46
## 2 | 2 | 35 | 20.96 | 21.08 | 35.54
## 3 | 3 | 46 | 27.54 | 27.71 | 63.25
## 4 | 4 | 39 | 23.35 | 23.49 | 86.75
## 5 | 5 trifft voll und ganz zu | 22 | 13.17 | 13.25 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich mache mir Sorgen, dass ich wegen meiner Inkompetenz mit Computern irreparable Schäden verursachen werde. (R101_13) <integer>
## # total N=167 valid N=166 mean=1.77 sd=1.12
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 95 | 56.89 | 57.23 | 57.23
## 2 | 2 | 38 | 22.75 | 22.89 | 80.12
## 3 | 3 | 16 | 9.58 | 9.64 | 89.76
## 4 | 4 | 10 | 5.99 | 6.02 | 95.78
## 5 | 5 trifft voll und ganz zu | 7 | 4.19 | 4.22 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Computer haben ihren eigenen Willen und gehen absichtlich immer dann kaputt, wenn ich sie benutze. (R101_14) <integer>
## # total N=167 valid N=166 mean=1.56 sd=0.96
##
## Value | Label | N | Raw % | Valid % | Cum. %
## --------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 110 | 65.87 | 66.27 | 66.27
## 2 | 2 | 33 | 19.76 | 19.88 | 86.14
## 3 | 3 | 14 | 8.38 | 8.43 | 94.58
## 4 | 4 | 4 | 2.40 | 2.41 | 96.99
## 5 | 5 trifft voll und ganz zu | 5 | 2.99 | 3.01 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Computer sind darauf aus, mich zu überlisten. (R101_15) <integer>
## # total N=167 valid N=166 mean=1.52 sd=0.94
##
## Value | Label | N | Raw % | Valid % | Cum. %
## --------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 112 | 67.07 | 67.47 | 67.47
## 2 | 2 | 36 | 21.56 | 21.69 | 89.16
## 3 | 3 | 10 | 5.99 | 6.02 | 95.18
## 4 | 4 | 2 | 1.20 | 1.20 | 96.39
## 5 | 5 trifft voll und ganz zu | 6 | 3.59 | 3.61 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich weine offen, wenn von zentraler Tendenz die Rede ist. (R101_16) <integer>
## # total N=167 valid N=166 mean=2.02 sd=1.29
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 84 | 50.30 | 50.60 | 50.60
## 2 | 2 | 33 | 19.76 | 19.88 | 70.48
## 3 | 3 | 22 | 13.17 | 13.25 | 83.73
## 4 | 4 | 15 | 8.98 | 9.04 | 92.77
## 5 | 5 trifft voll und ganz zu | 12 | 7.19 | 7.23 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich falle in ein Koma, wenn ich eine Gleichung sehe. (R101_17) <integer>
## # total N=167 valid N=166 mean=1.86 sd=1.16
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 88 | 52.69 | 53.01 | 53.01
## 2 | 2 | 41 | 24.55 | 24.70 | 77.71
## 3 | 3 | 19 | 11.38 | 11.45 | 89.16
## 4 | 4 | 9 | 5.39 | 5.42 | 94.58
## 5 | 5 trifft voll und ganz zu | 9 | 5.39 | 5.42 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: R stürzt immer ab, wenn ich versuche, es zu benutzen. (R101_18) <integer>
## # total N=167 valid N=166 mean=1.74 sd=1.07
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 94 | 56.29 | 56.63 | 56.63
## 2 | 2 | 42 | 25.15 | 25.30 | 81.93
## 3 | 3 | 15 | 8.98 | 9.04 | 90.96
## 4 | 4 | 9 | 5.39 | 5.42 | 96.39
## 5 | 5 trifft voll und ganz zu | 6 | 3.59 | 3.61 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Alle schauen mich an, wenn ich R benutze. (R101_19) <integer>
## # total N=167 valid N=166 mean=1.52 sd=0.98
##
## Value | Label | N | Raw % | Valid % | Cum. %
## --------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 117 | 70.06 | 70.48 | 70.48
## 2 | 2 | 26 | 15.57 | 15.66 | 86.14
## 3 | 3 | 13 | 7.78 | 7.83 | 93.98
## 4 | 4 | 5 | 2.99 | 3.01 | 96.99
## 5 | 5 trifft voll und ganz zu | 5 | 2.99 | 3.01 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich kann nicht schlafen, weil ich an Signifikanzen denke. (R101_20) <integer>
## # total N=167 valid N=166 mean=1.87 sd=1.26
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 97 | 58.08 | 58.43 | 58.43
## 2 | 2 | 29 | 17.37 | 17.47 | 75.90
## 3 | 3 | 16 | 9.58 | 9.64 | 85.54
## 4 | 4 | 13 | 7.78 | 7.83 | 93.37
## 5 | 5 trifft voll und ganz zu | 11 | 6.59 | 6.63 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich wache unter meiner Bettdecke auf und denke, dass ich unter einer Normalverteilung gefangen bin. (R101_21) <integer>
## # total N=167 valid N=166 mean=1.93 sd=1.41
##
## Value | Label | N | Raw % | Valid % | Cum. %
## --------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 104 | 62.28 | 62.65 | 62.65
## 2 | 2 | 16 | 9.58 | 9.64 | 72.29
## 3 | 3 | 18 | 10.78 | 10.84 | 83.13
## 4 | 4 | 9 | 5.39 | 5.42 | 88.55
## 5 | 5 trifft voll und ganz zu | 19 | 11.38 | 11.45 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Meine Freunde sind besser in R als ich. (R101_22) <integer>
## # total N=167 valid N=166 mean=2.86 sd=1.15
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 19 | 11.38 | 11.45 | 11.45
## 2 | 2 | 48 | 28.74 | 28.92 | 40.36
## 3 | 3 | 54 | 32.34 | 32.53 | 72.89
## 4 | 4 | 28 | 16.77 | 16.87 | 89.76
## 5 | 5 trifft voll und ganz zu | 17 | 10.18 | 10.24 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Wenn ich gut in Statistik bin, werden die Leute denken, ich sei ein Streber. (R101_23) <integer>
## # total N=167 valid N=166 mean=1.92 sd=1.28
##
## Value | Label | N | Raw % | Valid % | Cum. %
## -------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 96 | 57.49 | 57.83 | 57.83
## 2 | 2 | 25 | 14.97 | 15.06 | 72.89
## 3 | 3 | 18 | 10.78 | 10.84 | 83.73
## 4 | 4 | 17 | 10.18 | 10.24 | 93.98
## 5 | 5 trifft voll und ganz zu | 10 | 5.99 | 6.02 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
##
## RAQ: Ich mag Statistik, würde das aber nie vor meinen Freunden zugeben. (R101_24) <integer>
## # total N=167 valid N=166 mean=1.53 sd=0.90
##
## Value | Label | N | Raw % | Valid % | Cum. %
## --------------------------------------------------------------------
## -9 | nicht beantwortet | 0 | 0.00 | 0.00 | 0.00
## 1 | 1 trifft überhaupt nicht zu | 111 | 66.47 | 66.87 | 66.87
## 2 | 2 | 32 | 19.16 | 19.28 | 86.14
## 3 | 3 | 16 | 9.58 | 9.64 | 95.78
## 4 | 4 | 4 | 2.40 | 2.41 | 98.19
## 5 | 5 trifft voll und ganz zu | 3 | 1.80 | 1.81 | 100.00
## <NA> | <NA> | 1 | 0.60 | <NA> | <NA>
Cases <- DATEN |>
select(CASE, R101_01:R101_24) |>
na.omit()
Faktoren <- items |>
psych::factor.scores(f = m.ml.r, method = "Thurstone")
Faktoren_der_Faelle <- cbind(Cases, Faktoren$scores)
DATEN <- DATEN |>
left_join(Faktoren_der_Faelle, by = "CASE")
DATEN |> saveRDS("data/Stat_A-Befragung_mit_FA.RDS")