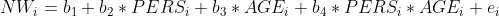6 GLM – Interaktionen

Veröffentlichungsdatum

2024-03-05

6.1 Die Folien zur Sitzung

Der Podcast

6.2 Interaktion mit Slope-Dummy

Eine Slope-Dummy ist ein Produkt aus einer metrischen Variable und einer Dummyvariabeblen. Durch diese Kombination wird es möglich, dass nicht nur der Mittelwert von zwei Gruppen unterschiedlich sein kann, sondern auch die Anstiege der Regressionsgeraden unterschiedlich sein können. Das bedeutet im Grunde, dass man prüfen kann, ob der Zusammenhang einer metrischen Variable für Gruppen unterschiedlich ist. Anders gesagt kann die Fragestellung beantwortet werden, ob zwei Gruppen sich in der Stärke des Zusammenhangs unterscheiden. Also zum Beispiel, ob ein Nachrichtenfaktor bei einer Rezipient:innengruppe anders wirkt (ein anderes Gewicht hat) als bei einer anderen Gruppe.

In der Grafik ist gut zu erkennen, dass die grüne Gruppe und die pinke Gruppe unterschiedliche Anstiege haben und damit die Lage der Werte besser abbilden kann, als würde man nur erlauben, dass die Mittelwerte unterschiedlich sind.

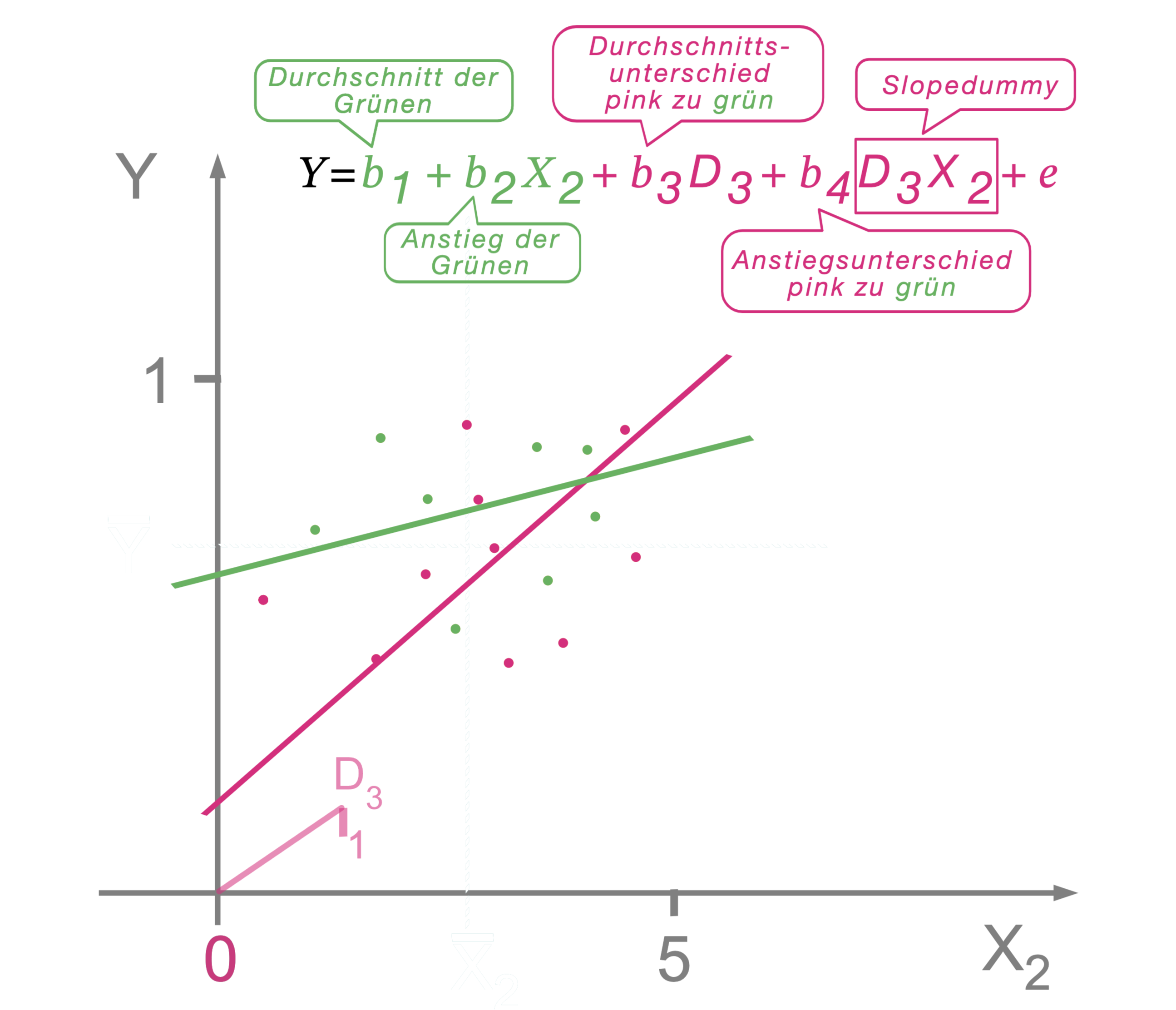
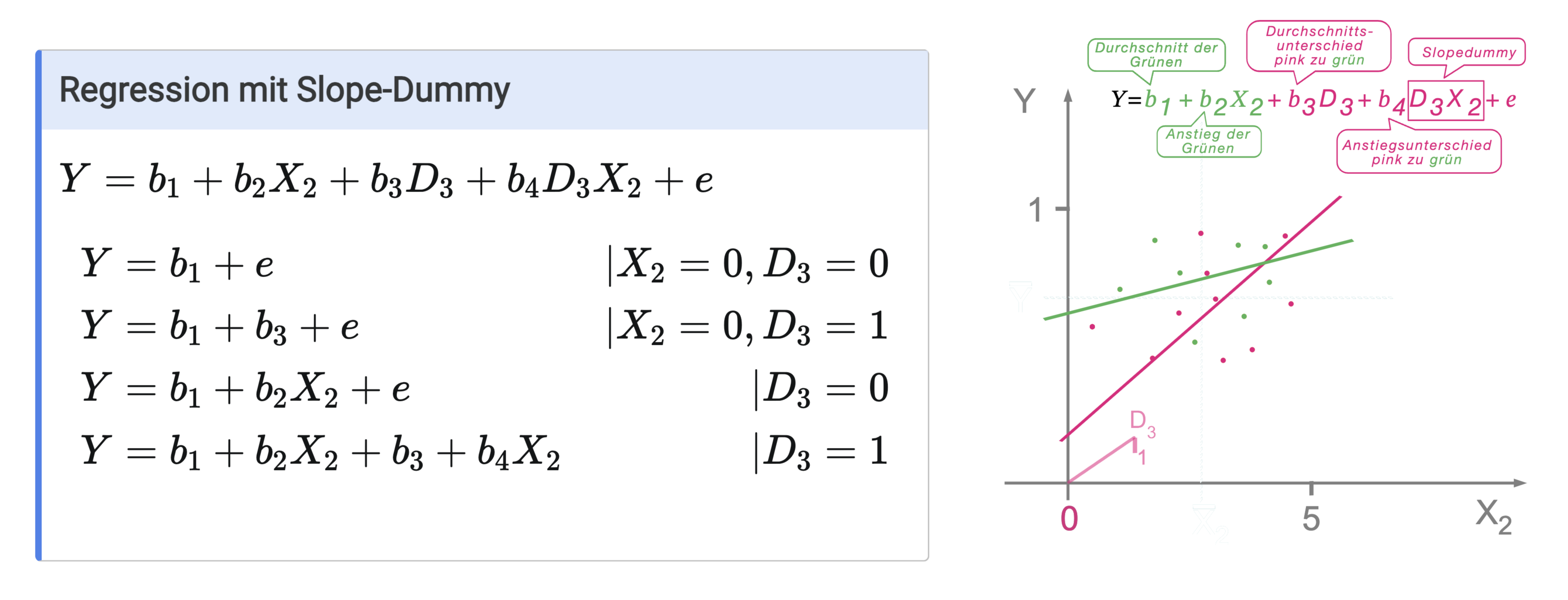
Das \(b_1\) steht für den Schnittpunkt mit der Y-Achse (\(X_2=\)) der 0-Gruppe (grün) und \(b_3\) für den Schnittpunkt der pinken mit der Y-Achse. Diese beiden Werte sind nicht ohne Weiteres interpretierbar und sorgen nur dafür, dass die Regressionsgeraden sich frei an die Werte der Gruppen anpassen könnnen. Interpretierbar wird das Ganze, wenn man die metrische Variable \(X_2\) zentriert, also in ihren Mittelwert verschiebt. Dann ist das \(b_1\) der Mittelwert der grünen 0-Gruppe und das \(b_3\) der Mittelwertunterschied zwischen der pinken 1-Gruppe und der 0-Gruppe.

In Worten bedeteutet das also:

Setzt man einzelne Werte gedanklich auf 0, wird die Formel jeweils klarer. Beachten Sie, dass auch das *1 weggelassen wird, wenn D = 1 ist.

6.3 Beispiel zu Videospielen und Aggression

Mit dem folgenden Beispiel läuft auch die Übung 2. Sie werden also selbst mit denselben Daten arbeiten. Dafür müssen sie zunächst geladen werden.

Wie Sie am Kopf der Datendatei sehen, besteht sie aus drei inhaltlichen Variablen und einer ID.

Agression: wurde auf einer breit angelegten Skala gemessen.
Vid_Games: wurde als Stunden pro Woche abgefragt.
Antisoziales Varhalten wurde ebenfalls mit einer Skala gemessen und kann daher hohe Werte annehmen und ist metrisch.

download.file(
  "http://www.discoveringstatistics.com/docs/ds_data_files/SPSS%20Data%20Files/Video%20Games.sav", 
  "data/Video_Games.sav", quiet = TRUE)

DATEN <- haven::read_spss("data/Video_Games.sav")

head(DATEN)
## # A tibble: 6 × 4
##      ID Aggression Vid_Games CaUnTs
##   <dbl>      <dbl>     <dbl>  <dbl>
## 1    69         13        16      0
## 2    55         38        12      0
## 3     7         30        32      0
## 4    96         23        10      1
## 5   130         25        11      1
## 6   124         46        29      1

6.4 Zusammenhang Videospiele und Aggression

Die Variable «CaUnTs» wird zunächst in einer kategoriale Variable umkodiert, wobei die 1 für geringes antisoziales Verhalten steht, die 2 für mittleres und die 3 für hohes. Ganz aggressionsfrei ist kaum jemand, aber etwa ein Viertel der Befragten zeigte eher tiefe Werte in der neu gebildeten Variable «Antisozial». Die meisten liegen in der Mitte (62%) und zum Glück nur wenige bei hohen Werten für antisoziales Verhalten (14%).

DATEN <- DATEN  |>
  mutate(Anti_Sozial = case_match(CaUnTs,
    c(0:10) ~ 1,
    c(11:30) ~ 2,
    c(31:200) ~ 3, 
    .default = NA
  )) |>
  sjlabelled::var_labels(Anti_Sozial = "Antisoziales Verhalten")

DATEN |> sjmisc::frq(Anti_Sozial)
## Antisoziales Verhalten (Anti_Sozial) <numeric> 
## # total N=442 valid N=442 mean=1.89 sd=0.61
## 
## Value |   N | Raw % | Valid % | Cum. %
## --------------------------------------
##     1 | 108 | 24.43 |   24.43 |  24.43
##     2 | 273 | 61.76 |   61.76 |  86.20
##     3 |  61 | 13.80 |   13.80 | 100.00
##  <NA> |   0 |  0.00 |    <NA> |   <NA>

R-Code

# Speichere in dem Datensatz Video_Games_AS_gering man nur die Fälle mit mittlerer 
# oder geringem Antisozialem Verhalten.

Video_Games_AS_gering <- DATEN  |>
  filter(CaUnTs < 31)

# Mache einen Scatterplot (geom_point) für Vid_Games und Agression, unterteilt nach 
# Anti_Sozial und lege da mit geom_smooth jeweils eine Regressionsgerade rein.

Video_Games_AS_gering  |> 
  ggplot2::ggplot(aes(x = Vid_Games, y = Aggression, color = as.factor(Anti_Sozial))) +
  geom_point()+ 
  scale_color_manual(values=c(c(Farben[3], Farben[4]))) + 
  geom_smooth(method=lm, se=FALSE, fullrange=TRUE) + 
  theme_minimal()
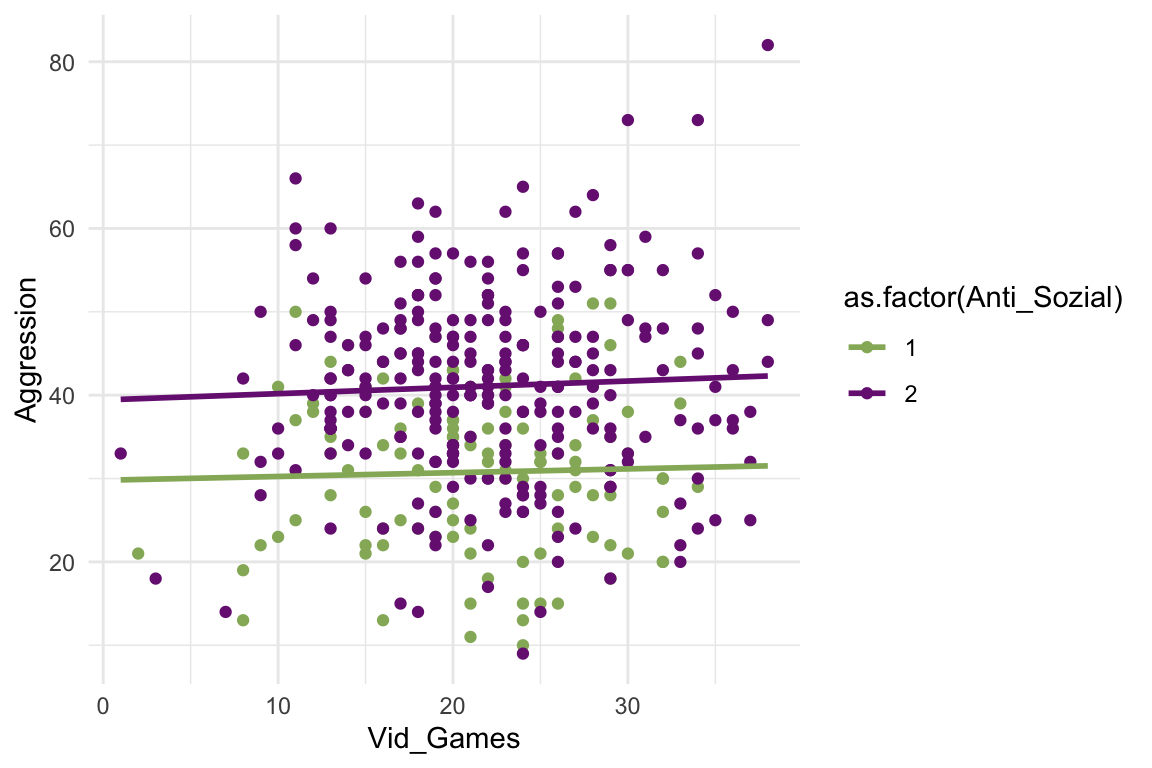
## `geom_smooth()` using formula = 'y ~ x'

In der Grafik sind die Punktverteilungen gut zu sehen und auch, dass die Gruppe mit hohem Werten in «Antisozial» einen deutlich stärkeren Zusammenhang zwischen der Nutzung von Videospielen und Aggression zeigen.

[Mehr wird hier erstm nicht gespoilert, weil die Interpreltationen der Werte Teil der Übung sind 😃]

6.4.1 Grafik Videogames

R-Chunk

DATEN <- DATEN  |>
  mutate(Anti_Soz_hoch = case_match(Anti_Sozial,
   3 ~ 1,
   .default = 0
  ), 
  Anti_Soz_mittel = case_match(Anti_Sozial, 
  2 ~ 1, 
  .default = 0))

DATEN  |> sjmisc::frq(Anti_Soz_hoch)
## Anti_Soz_hoch <numeric> 
## # total N=442 valid N=442 mean=0.14 sd=0.35
## 
## Value |   N | Raw % | Valid % | Cum. %
## --------------------------------------
##     0 | 381 | 86.20 |   86.20 |  86.20
##     1 |  61 | 13.80 |   13.80 | 100.00
##  <NA> |   0 |  0.00 |    <NA> |   <NA>

DATEN  |>
  ggplot2::ggplot(aes(x = Vid_Games, y = Aggression, 
                color = as.factor(Anti_Soz_hoch))) +
  geom_point()+ 
  scale_color_manual(values=c(c(Farben[3], Farben[4]))) + 
  geom_smooth(method=lm, se=FALSE, fullrange=TRUE) + 
  theme_minimal()
## `geom_smooth()` using formula = 'y ~ x'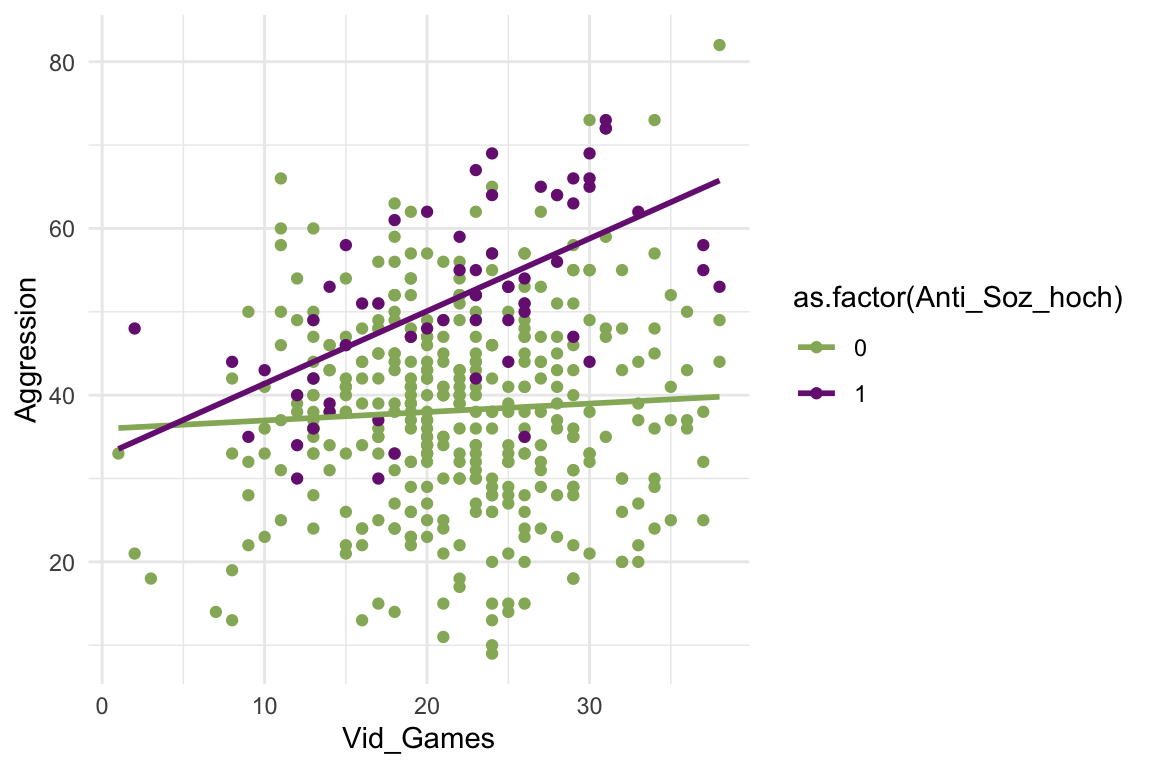

Zusammenhang Videospiele zu Aggression für Menschen mit hohem vs. geringerem antisozialen Verhalten

6.4.2 Multikollinearität bei Slope-Dummys und Lösungsansätze

Q&A: Welches besondere Problem gibt es bei Slop-Dummys mit Multikollinearität und wie löst man es?

Die Slope Dummy ist das Produkt aus der ursprünglichen Dummy und der metrischen. Da die Metrische und die Dummy aber auch noch im Modell sein müssen, korreliert die Slope-Dummy, wie Sie richtig sagen, mit der Metrischen, aber eben auch mit der Dummy, da die Slope-Dummy bei allen Fällen eine 0 hat, wo die Dummy eine 0 hat und immer dann, wenn die Slope-Dummy positiv ist, die Dummy auch positiv ist (eine 1) hat. Das ist das besondere (eher technische) Problem der Multikollinearität der Slope-Dummy. Das können wir lösen, indem wir die Metrische vorher zentrieren. Dann ist die Slope-Dummy zwar immernoch 0, wenn die Dummy 0 ist, aber sie streut um 0, wenn die Dummy 1 ist. Damit gibt es für den Fall diese technische Multikollinearität nicht mehr. Es bleibt noch, dass die Slope-Dummy mit der Metrischen identisch ist, wenn die Dummy 1 ist. Das ist dann problematisch, wenn die 1-en viel sind, weil die Metrische dann in vielen Fällen mit der Slope-Dummy übereinstimmt. Das können wir lösen, indem wir die Dummy umdrehen (und gut im Kopf behalten, dass wir sie umgedreht haben), also die selteneren 0-en zur 1 machen und die 1-en zur 0. Wir würden also nicht

Beispiel: Wenn wir die Wahrscheinlichkeit zu wählen damit vorhersagen wollten, dass jemand gebürtige:r Schweier:in ist und wie viele Minuten Nachrichten er:sie in der Woche konsumiert, wäre die Annahme sicher, dass gebürtige Schweizer:innen eher wählen gehen und der Umfang des Nachrichtenkonsums auch positiv mit der Wahrscheinlichkeit zu tun hat, dass jemand wählen gehen würde Variable WAHL. Wenn wir dann noch annehmen, dass der Umfang des Nachrichtenkonsums einen stärkeren Zusammenhang für Schweizerinnen hat als auf die Nicht-Schweizer:innen, dann bauen wir noch die Interaktion ein CHNachrichten_Dauer. Die Interaktionsvariable CHNachrichten_Dauer korelliert dann mit CH und Nachrichten_dauer. Wenn wir vorher Nachrichten_dauer zentrieren (also minus ihrem Mittelwert), dann korelliert CHNachrichten_Dauer nicht mehr mit CH, aber noch recht stark mit Nachrichten_dauer. Also kodieren wir um und machen aus der Dummy CH die Dummy Nicht_CH. Dann korelliert die Nicht_CH kaum noch mit der Nicht_CHNachrichten_Dauer. Wenn die Slope-Dummy dann signifikant negativ ist, würden wir sagen, dass der Zusammenhang zwischen dem Umfang der Nachrichtennutzung bei Nicht-Schweizer:innen geringer ist als bei gebürtigen Schweizer:innen.

Antwortsatz in der Klausur: Da die Slope-Dummy stark mit der Dummy korelliert, wenn die Metrische immer im positiven (oder negativen) Bereich liegt, gibt es hohe Multikollinearität, die dadurch verringert werden kann, dass die Metrische vorher zentriert wird. Überwiegen in der Dummy die 1-en deutlich, ist die Multikollinearität zwischen der Metrischen und der Slope-Dummy eventuell noch ein Problem. Dann sollte die Dummy umkodiert werden.

6.5 Regression (unzentriert)

R-Chunk


Modell4 <- lm(Aggression ~ Vid_Games + Vid_Games * Anti_Soz_hoch, data = DATEN)

olsrr::ols_vif_tol(Modell4)
##                 Variables Tolerance      VIF
## 1               Vid_Games 0.8318770 1.202101
## 2           Anti_Soz_hoch 0.1049793 9.525692
## 3 Vid_Games:Anti_Soz_hoch 0.1024746 9.758512

sjPlot::tab_model(Modell4, 
                  show.ci = FALSE,
                  show.std = TRUE, # zeige die standardisierten Koeffizienten
                  show.est = TRUE, # zeige die unstandardisierten estimates
                  show.r2 = TRUE # zeige R^2
                  )

	Agression
Predictors	Estimates	std. Beta	p	std. p
(Intercept)	35.95	-0.00	<0.001	0.968
Video Games(Hours per week)	0.10	0.11	0.238	0.008
Anti Soz hoch	-3.28	0.37	0.501	<0.001
Vid_Games:Anti_Soz_hoch	0.77	0.15	<0.001	<0.001
Observations	442
R² / R² adjusted	0.183 / 0.177

6.6 Regression nach Zentrierung

R-Chunk

DATEN |>
  summarize(Aggressions_Mittel = mean(Aggression, na.rm = TRUE), .by = Anti_Soz_hoch) 
## # A tibble: 2 × 2
##   Anti_Soz_hoch Aggressions_Mittel
##           <dbl>              <dbl>
## 1             0               38.2
## 2             1               51.9

51.9 - 38.2
## [1] 13.7

# zentriere Vid_Games (Mittelwert = 0):
DATEN_z <- DATEN %>% 
  mutate(Vid_Games = Vid_Games - mean(Vid_Games, na.rm = TRUE)) 

Modell4 <- lm(Aggression ~ Vid_Games + 
                            Anti_Soz_hoch + 
                            Vid_Games * Anti_Soz_hoch,
                            data = DATEN_z)

olsrr::ols_vif_tol(Modell4)
##                 Variables Tolerance      VIF
## 1               Vid_Games 0.8318770 1.202101
## 2           Anti_Soz_hoch 0.9993801 1.000620
## 3 Vid_Games:Anti_Soz_hoch 0.8314800 1.202675

sjPlot::tab_model(Modell4, 
                  show.ci = FALSE,
                  show.std = TRUE, # zeige die standardisierten Koeffizienten
                  show.est = TRUE, # zeige die unstandardisierten estimates
                  show.r2 = TRUE, # zeige R^2
                  show.fstat = TRUE
                  )

	Agression
Predictors	Estimates	std. Beta	p	std. p
(Intercept)	38.17	-0.00	<0.001	0.968
Video Games(Hours per week)	0.10	0.11	0.238	0.008
Anti Soz hoch	13.52	0.37	<0.001	<0.001
Vid_Games:Anti_Soz_hoch	0.77	0.15	<0.001	<0.001
Observations	442
R² / R² adjusted	0.183 / 0.177

6.7 Kategoriale UV

R-Chunk

Modell5 <- lm(Aggression ~ Vid_Games + Anti_Soz_hoch + Anti_Soz_mittel +
                Vid_Games * Anti_Soz_hoch + Vid_Games * Anti_Soz_mittel,
              data = DATEN_z)

olsrr::ols_vif_tol(Modell5)
##                   Variables Tolerance      VIF
## 1                 Vid_Games 0.2266636 4.411824
## 2             Anti_Soz_hoch 0.7390622 1.353066
## 3           Anti_Soz_mittel 0.7373241 1.356256
## 4   Vid_Games:Anti_Soz_hoch 0.5739909 1.742188
## 5 Vid_Games:Anti_Soz_mittel 0.2730809 3.661919

sjPlot::tab_model(Modell5, 
                  show.std = TRUE, # zeige die standardisierten Koeffizienten
                  show.est = TRUE, # zeige die unstandardisierten estimates
                  show.ci = FALSE,
                  show.r2 = TRUE, # zeige R^2
                  show.fstat = TRUE,
                  string.est = "b",
                  string.std = "std. b"
                  )

	Agression
Predictors	b	std. b	p	std. p
(Intercept)	30.79	-0.00	<0.001	0.958
Video Games(Hours per week)	0.05	0.10	0.766	0.015
Anti Soz hoch	20.90	0.57	<0.001	<0.001
Anti Soz mittel	10.29	0.40	<0.001	<0.001
Vid_Games:Anti_Soz_hoch	0.82	0.16	<0.001	<0.001
Vid_Games:Anti_Soz_mittel	0.03	0.01	0.865	0.865
Observations	442
R² / R² adjusted	0.299 / 0.291

7 Interaktion zweier metrischer Variablen

Interaktion zweier metrischer Variablen (in Worten)

R-Chunk


# verändere alle numerischen Variablen, indem sie z-transformiert werden (scale)
DATEN_z <- DATEN  |>
  mutate(across(everything(), ~.x - mean(.x, na.rm = TRUE))) 

Modell5 <- lm(Aggression ~ Vid_Games * CaUnTs,
              data = DATEN_z)

olsrr::ols_vif_tol(Modell5)
##          Variables Tolerance      VIF
## 1        Vid_Games 0.9930553 1.006993
## 2           CaUnTs 0.9974262 1.002580
## 3 Vid_Games:CaUnTs 0.9950094 1.005016

sjPlot::tab_model(Modell5, 
                  show.std = TRUE, # zeige die standardisierten Koeffizienten
                  show.est = TRUE, # zeige die unstandardisierten estimates
                  show.ci = FALSE,
                  show.r2 = TRUE, # zeige R^2
                  show.fstat = TRUE,
                  string.est = "b",
                  string.std = "std. b"
                  )

	Agression
Predictors	b	std. b	p
(Intercept)	-0.09	-0.01	0.854
Video Games(Hours per week)	0.17	0.09	0.014
Callous Unemotional Traits	0.76	0.58	<0.001
Vid_Games:CaUnTs	0.03	0.14	<0.001
Observations	442
R² / R² adjusted	0.377 / 0.373

Interaktionen zwischen metrischen Variablen zeigen an, inwiefern der Anstieg der einen UV mit dem grösser werden der anderen UV steigt. Also:

Die Nutzung von Videogames hat einen signifikanten, aber sehr geringen Einfluss auf Aggression.
Antisoziale Persönlichkeitsmerkmale korrelieren stark mit Aggression
Je höher die antisozialen Persönlichkeitsmerkmale, desto stärker wird der Zusammenhang zwischen der Nutzung von Video-Games und Aggression
und: Je mehr Videospiele jemand spielt, desto grösser wird der Zusammenhang zwischen Antisozialen Merkmalen und Aggression.

LEF 6

Essayfragen 6

E6.1 Was ist eine Slope-Dummy-Variable?

E6.2 Wenn Sie die Hypothese haben, dass der Nachrichtenfaktor «Personalsierung» stärker wirkt, je älter die Befragten sind, wie würden Sie das Regressionsmodell formulieren (Gleichung)? Sie können auch die Modellschreibweise von R verwenden, also lm().

Formel-Lösung E6.2

E6.3 Warum ist beim Rechnen mit Slope-Dummys die Multikollinearität ein besonderes Problem? Wie können Sie das bei Slope-Dummys (und nur hier) lösen?

E6.4 Zeichnen Sie ein typisches Beispiel für einen Zusammenhang, den man mit einer Slope-Dummy modellieren würde. (Tipp: Es braucht ein Koordinatensystem und dann zeichnen Sie da Punkte mit unterschiedlichen Farben und Regressionsgeraden rein.)

Lösung E6.4

E6.5 (war fast wie 6.3 und wurde mit ihr zusammengelegt)

E6.6 Wie bilden Sie in R eine Slope-Dummy (Interaktion zwischen einer Dummy und einer Metrischen)

MC-Fragen 6

MC 6.1.

MC 6.1: Sind folgende Aussagen richtig oder falsch?

MC_6_1 = [
    ["Eine Slope-Dummy ist eine Interaktion", "richtig"],
    ["Slope-Dummys geben den Anstieg der Dummyvariablen wieder.", "falsch"],
    ["Interaktionen von Variablen werden als Produkt der Variablen gebaut.", "richtig"],
    ["In R müssen die Interaktionen als Differntialgleichung erstellt werden.", "falsch"]
]

viewof answers_6_1 = quizInput({
  questions: MC_6_1,
  options: ["richtig", "falsch"]
})

Punkte_6_1 = {
const Sum = 
    (answers_6_1[0] == MC_6_1[0][1])*1 + 
    (answers_6_1[1] == MC_6_1[1][1])*1 + 
    (answers_6_1[2] == MC_6_1[2][1])*1 + 
    (answers_6_1[3] == MC_6_1[3][1])*1 

var Punkte_6_1 = Sum - 2
if (Punkte_6_1 < 1) {Punkte_6_1 = 0}
return(Punkte_6_1)
}

Punkte:

MC 6.2.

MC 6.2: Sind folgende Aussagen richtig oder falsch?

MC_6_2 = [
    ["Wenn man Interaktionen im Modell hat, müssen auch immer die Haupteffekte im Modell sein.", "richtig"],
    ["Wenn man Slope-Dummys baut, muss die Referenzkategorie mit in das Modell.", "falsch"],
    ["Das b_1 einer Regression mit Slope-Dummy gibt den Mittelwert für die 0-Gruppe wieder.", "falsch"],
    ["Das BETA einer Slope-Dummy ist nicht interpretierbar.", "falsch"]
]

viewof answers_6_2 = quizInput({
  questions: MC_6_2,
  options: ["richtig", "falsch"]
})

Punkte_6_2 = {
const Sum = 
    (answers_6_2[0] == MC_6_2[0][1])*1 + 
    (answers_6_2[1] == MC_6_2[1][1])*1 + 
    (answers_6_2[2] == MC_6_2[2][1])*1 + 
    (answers_6_2[3] == MC_6_2[3][1])*1 

var Punkte_6_2 = Sum - 2
if (Punkte_6_2 < 1) {Punkte_6_2 = 0}
return(Punkte_6_2)
}

Punkte:

MC 6.3.

MC 6.3: Sind folgende Aussagen richtig oder falsch?

MC_6_3 = [
    ["Bestehen in einer Regression die UVs aus einer Dummy und zwei metrischen Variablen, ergeben sich zwei Ebenen, die sich nicht berühren.", "richtig"],
    ["In einer Regression mit einem Faktor der drei Ausprägungen hat und einer metrischen Variablen, haben die drei Gruppen unterschiedliche Anstiege.", "falsch"],
    ["Die hohe (technische) Multikollinearität durch Dummyvariablen lässt sich durch z-Transformation der metrischen UVs reduzieren.", "richtig"],
    ["In R würde eine Slope-Dummy nach folgendem Schema gebaut: lm(AV ~ Dummy + Metrische + Dummy * Metrische, data = DATEN)", "richtig"]
]

viewof answers_6_3 = quizInput({
  questions: MC_6_3,
  options: ["richtig", "falsch"]
})

Punkte_6_3 = {
const Sum = 
    (answers_6_3[0] == MC_6_3[0][1])*1 + 
    (answers_6_3[1] == MC_6_3[1][1])*1 + 
    (answers_6_3[2] == MC_6_3[2][1])*1 + 
    (answers_6_3[3] == MC_6_3[3][1])*1 

var Punkte_6_3 = Sum - 2
if (Punkte_6_3 < 1) {Punkte_6_3 = 0}
return(Punkte_6_3)
}

Punkte:

MC 6.4.

MC 6.4: Sind folgende Aussagen richtig oder falsch?

MC_6_4 = [
    ["Wenn das b einer Slope-Dummy negativ ist, hat die 1-Gruppe einen tieferen Anstieg als die 0-Gruppe.", "richtig"],
    ["Wenn es im Modell eine Slope-Dummy gibt, ist das b der Dummy nicht mehr der Mittelwertunterschied zwischen den Gruppen.", "richtig"],
    ["Zwei metrische Variablen können auch einen Interaktionseffekt haben.", "richtig"],
    ["Gibt es drei UV, kann jede mit jeder und alle zusammen Interaktionseffekte haben.", "richtig"]
]

viewof answers_6_4 = quizInput({
  questions: MC_6_4,
  options: ["richtig", "falsch"]
})

Punkte_6_4 = {
const Sum = 
    (answers_6_4[0] == MC_6_4[0][1])*1 + 
    (answers_6_4[1] == MC_6_4[1][1])*1 + 
    (answers_6_4[2] == MC_6_4[2][1])*1 + 
    (answers_6_4[3] == MC_6_4[3][1])*1 

var Punkte_6_4 = Sum - 2
if (Punkte_6_4 < 1) {Punkte_6_4 = 0}
return(Punkte_6_4)
}

Punkte:

MC 6.5.

MC 6.5: Sind folgende Aussagen richtig oder falsch?

MC_6_5 = [
    ['Gibt es nur eine metrische UV, muss diese in mehrere Dummys umkodiert werden, um Slope-Dummys bauen zu können.', "falsch"],
    ["Wenn eine Slope-Dummy signifikant ist, hat die 1-Gruppe immer einen signifikant von 0 verschiedenen Anstieg.", "falsch"],
    ["Wenn die Dummy-Variable, die für eine Slope-Dummy verwendet werden soll, mehr als 5 Ausprägungen hat, dann kann sie auch als metrisch betrachtet werden.", "falsch"],
    ["Beim R-Output zu Regressionskoeffizienten haben viele Pakete verschiedene Kennzeichnungen. Man muss also sehr genau hinschauen, was womit gemeint ist.", "richtig"]
]

viewof answers_6_5 = quizInput({
  questions: MC_6_5,
  options: ["richtig", "falsch"]
})

Punkte_6_5 = {
const Sum = 
    (answers_6_5[0] == MC_6_5[0][1])*1 + 
    (answers_6_5[1] == MC_6_5[1][1])*1 + 
    (answers_6_5[2] == MC_6_5[2][1])*1 + 
    (answers_6_5[3] == MC_6_5[3][1])*1 

var Punkte_6_5 = Sum - 2
if (Punkte_6_5 < 1) {Punkte_6_5 = 0}
return(Punkte_6_5)
}

Punkte:

Punkte_6_max = 10

Punkte_6_Gesamt = Punkte_6_1 + Punkte_6_2 + Punkte_6_3 + Punkte_6_4 + Punkte_6_5

Prozent_6_Gesamt = round(100*Punkte_6_Gesamt/Punkte_6_max, 0)

Note_6_grob = round((round(Punkte_6_Gesamt/Punkte_6_max,1)*10+2)/2, 1)

Insgesamt von Punkten, was % und etwa einer entspricht.

round = (n, places) => {
  if (!places) return Math.round(n);
  const d = 10 ** places;
  return Math.round(n * d) / d;
}

function quizInput({ questions, options}) {
  let answers = questions.map(() => null);
  let root = htl.html`<div
      style="
        display: grid;
        grid-template-columns: 10% 10% 70% 10%;"
    >
      ${options.map(
        (opt) => htl.html`<div style="font-weight: bold; font-size: HUGE">${opt}</div>`
      )}
      <div style="font-weight: bold">Aussagen</div>
      <div style="font-weight: bold"></div>
      ${Array.from(questions.entries(), ([i, [question, correct]]) =>
        quizInputRow({
          question,
          options,
          correct,
          onChange: (newAnswer) => {
            answers[i] = newAnswer;
            root.value = answers;
            root.dispatchEvent(new CustomEvent("input"));
          }
        })
      )}
    </div>`;
  root.value = answers;
  return root;
}

function quizInputRow({
  question,
  options,
  correct,
  onChange = () => {}
}) {
  let root = htl.html`<div>`;

  function setAnswer(answer, initial = false) {
    morph(
      root,
      htl.html`<div style="display: contents"> 
      <form style="display: contents">
        ${options.map(
          (opt) =>
            htl.html`<label>&emsp;</label> 
            <input  
              name=${question} &emsp;
              type="radio"
              value="${opt}"
              checked=${opt === answer}
              onChange=${() => setAnswer(opt)}
            >
            </input>`
        )}
      </form>
      <div>${question}</div>
      <div> &emsp; ${
       answer === null ? "" : answer === correct ? "💚" : "❌"
      }</div>
    </div>`
    );

    root.value = answer;
    if (!initial) {
      root.dispatchEvent(new CustomEvent("input"));
      onChange(answer);
    }
  }

  setAnswer(null, true);
  return root;
}

morph = require("https://bundle.run/nanomorph@5.4.2")

MathJax = require("https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.5/MathJax.js?config=TeX-AMS_CHTML")
  .catch(() => window.MathJax)
  .then(MathJax => {
    MathJax.Hub.Config({
      CommonHTML: { scale: 110 }, // scaling to get the same size as katex (but katex still has more spacing between lines...)
      tex2jax: { inlineMath: [["$", "$"], ["\\(", "\\)"]] },
      displayMath: [["$$", "$$"], ["\\[", "\\]"]],
      processEscapes: true,
      TeX: { extensions: ["autoload-all.js"] },
    });
    return new Promise(resolve =>
      MathJax.Hub.Register.StartupHook("End", () => resolve(MathJax))
    );
  })