Q_2_0 = [
["Varianzanalyse", "richtig"],
["Regression", "richtig"],
["Univariate Statistik", "falsch"],
["Korrelation", "falsch"]
]
viewof answer_Q_2_0 = quizInput({
questions: Q_2_0,
options: ["richtig", "falsch"]
})
Punkte_Q_2_0 = {
const Sum =
(answer_Q_2_0[0] == Q_2_0[0][1])*1 +
(answer_Q_2_0[1] == Q_2_0[1][1])*1 +
(answer_Q_2_0[2] == Q_2_0[2][1])*1 +
(answer_Q_2_0[3] == Q_2_0[3][1])*1
var Punkte_Q_2_0 = Sum - 2
if (Punkte_Q_2_0 < 1) {Punkte_Q_2_0 = 0}
return(Punkte_Q_2_0)
}2 GLM – Regression
Die Folien zur Sitzung
Der Vorlesungsmitschnitt
2.1 Das lineare Modell (GLM)
2.1.1 Die Idee vom Modell
Für das Ergebnis der Datenerhebung wird ein Modell entworfen, das Zusammenhänge einfach darstellt. Da das Modell nie zu 100% das Ergebnis treffen wird, bleibt ein Rest, den wir Modellfehler oder einfach Fehler nennen.
Das lineare Modell ist die Basis von fast allem. Auch was Sie schon kennen, wird unter dem Konzept «lineares Modell» zusammengefasst:
- Varianzanalyse
- (Korrelation ist auch linear, aber eigentlich kein Modell)
- Regression
Das lineare Modell ist auch nicht auf lineare Zusammenhänge beschränkt. Es kann sehr gut mit kurvilinearen Zusammenhängen umgehen. Also, wenn zum Beispiel bei einer Gesamtnachrichtenlage mit sehr hohem Nachrichtenwert der Umfang des Medienkonsums steigt. Irgendwann erfährt diese Wirkung einen Deckeneffekt, weil niemand auf Dauer 24h am Tag Medien konsumieren kann. Vielleicht steigt der Nachrichtenkonsum mit dem Nachrichtenwert sogar Anfangs exponentiell (wie Coronazahlen) und hat dann bald einen Umkehrpunkt und strebt gegen ein mögliches Maximum. Selbst solche komplexeren Zusammenhänge können in einem linearen Modell dargestellt werden.
Die höhere Statistik wie Strukturgleichungsmodelle, Zeitreihenanalysen (Forcastings oder Laten-Growth-Curve-Modelle) bauen alle auf dem linearen Modell auf. Und auch Computational Science nutzt Modelle und zwar überwiegend als Basis die linearen Modelle.
2.2 Regression Einführung
Die Regression ist das einfachste und gleichzeitig mächtigste Werkzeug multivariater Datenanalyse. Aus den Kovarianzen mehrerer Variablen wird eine Funktion mit wenigen Kennwerten berechnet. Diese Kennwerte geben Auskunft darüber, wie etwas, das wir erklären wollen mit Dingen zusammenhängt, von denen wir glauben (hypothetisch annehmen), dass Sie Erklärungen liefern können. Man muss also vorher sagen, was man erklären will und womit man es erklären will. Die zu erklärende Grösse nennt man in der Sozialwissenschaft (und anderen Disziplinen): abhängige Variable (AV oder DV) und die Erklärungsgrössen nennt man: unabhängige Variablen (UV oder IV).
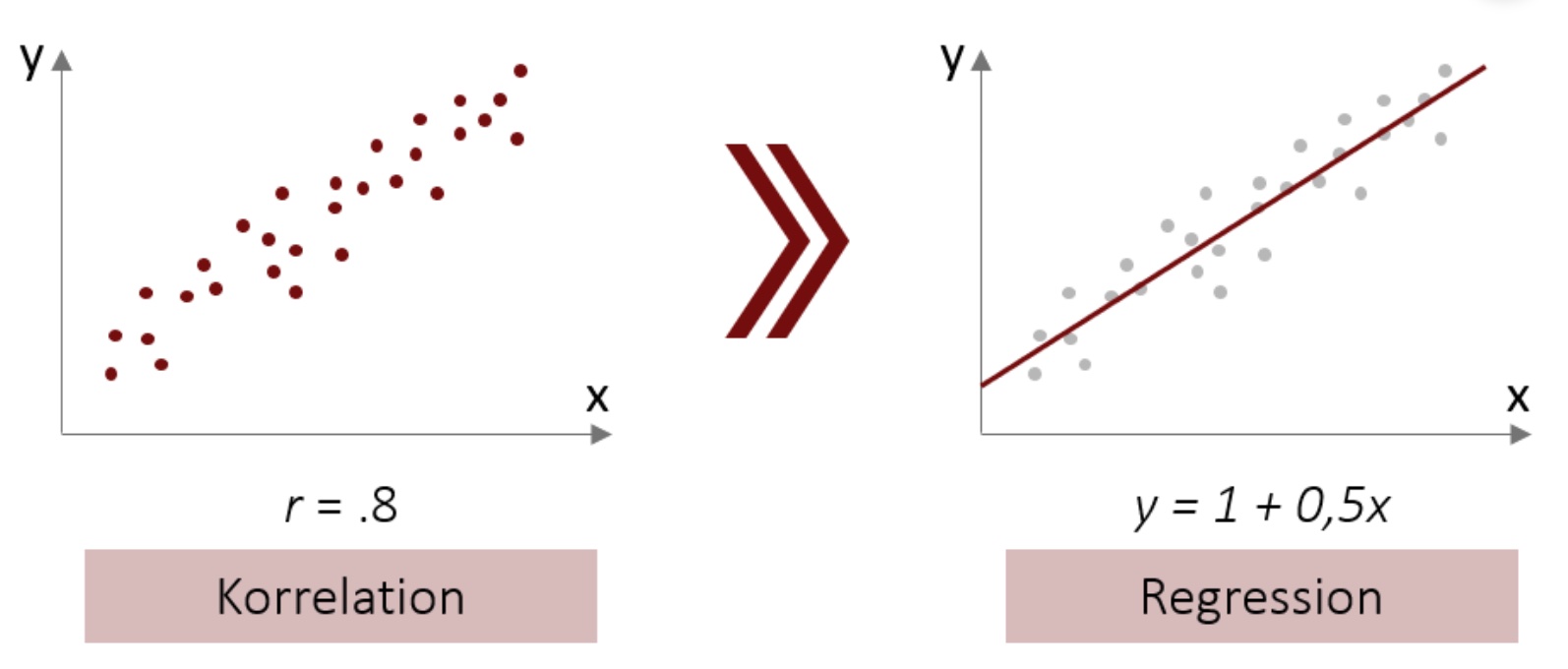
Die Regression baut auf Kovarianzen auf (bzw. Korrelationen, die wir uns besser vorstellen können). Die Regressionsgerade wird bei einer bivariaten Regression durch eine Konstante (in der Abbildung Abbildung 2.1 ist sie 1) und einem Anstieg je Variable gekennzeichnet (in der Abbildung ist es 0,5 für die eine UV = x).
2.2.1 Notation der (multivariaten) Regression
Auch wenn es sinnvoll war, bei der bivariaten Regression die Konstante «a» zu nennen, soll ab jetzt die Bezeichnung der Regressionskoeffizienten etwas geändert werden:
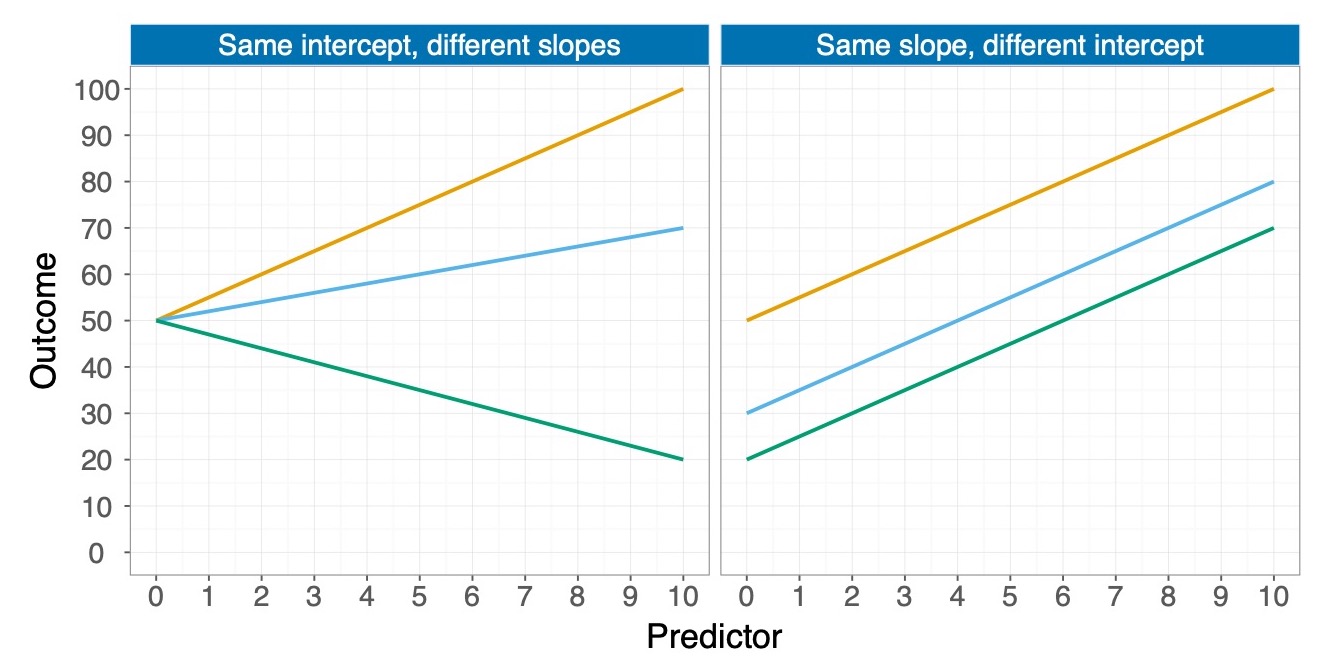
Das bedeutet, dass bei einer bivariaten Regression zwei b’s die Lage der Regressionsgeraden bestimmen: Das ist zum einen die Konstante \(b_1\) und zum anderen der Anstieg \(b_2\) für die Gerade. In der Abbildung 2.2 sehen Sie links zwei Regressionsgeraden mit unterschiedlichen \(b_2\) (rot positiv und grün negativ). Auf der rechten Seite sehen Sie drei Regressionsgeraden mit unterschiedlichen \(b_1\), wobei das b der roten Gerade am grössten ist (knapp 70), grün am kleinsten (bischen über 20) und blau in der Mitte liegt (knapp 40).
2.3 Das Modell und die Regressionsgleichung als Schätzung
Die formelle Schreibweise eines Regressionsmodells enthält griechische Buchstaben um zu signalisieren, dass es sich hier um unbekannte Grössen, die Parameter in der Grundgesamtheit, handelt. So lange wir über die Qualität und die Eigenschaften von Regressionsrechnungen sprechen, wird uns der Unterschied zwischen \(\beta\)’s und b’s interessieren.
Als Gleichung heisst das, dass die Abhängige Variable \(Y_i\) durch eine gewichtete Summe (siehe Formel Gleichung 2.1) von einer oder mehreren unabhängigen Variablen erklärt wird. Diese UVs werden in der Regel mit X gekennzeichnet und weil es mehrere davon geben kann, werden sie durchnummeriert. Also mit dem Subscript i für das Durchzählen werden sie griechisch für die Parameter als \(\beta_2X_{i2}\) bezeichnet oder eben als \(\beta_3X_{i3}\) usw. Dann gibt es noch den Rest \(U_i\). Das ist also das theoretische statistische Modell, dessen Parameter wir mit Kennwerten schätzen wollen.
\[ Y_i = \beta_1 + \beta_2X_{i2} + \beta_3X_{i3} + U_i \tag{2.1}\]
Wenn man mal genau schaut was nach der Stichprobenziehung eigentlich noch variabel ist, dann wird klar, dass die \(Y_i\) in der Datenerhebung gemessen wurden und damit Werte enthalten, die wir nicht mehr ändern. Das Gleiche gilt für die \(X_i\)-Werte der Variablen \(X_2\) und \(X_3\). Also sind diese Grössen eigentlich keine «Variablen» mehr, sondern längst durch echte Werte «fixiert». Zu schätzen sind nur die b’s, also \(b_1\), \(b_2\) und \(b_3\) (wie in Gleichung 2.2). Wenn wir die Regressionskoeffizienten, die b’s in unserer Stichprobe, berechnet haben, müssen wir uns noch fragen, wie gut, also unverzerrt und genau sie die unbekannten Parameter (\(\beta\)S) messen, also – etwas technischer ausgedrückt – ob die b die \(\beta\) erwartungstreu und effizient schätzen. Dafür gibt es einige Voraussetzungen, die wir uns später [in Kapitel noch nicht da] noch anschauen werden. Am Ende der Formel steht das \(e_i\) für die Fehler, also den unerklärten Rest der Varianz, der zwischen den durch das Modell geschätzten Werten (gekennzeichnet mit einem Dach als \(\hat{Y_i}\)) und den gemessenen Werten liegt. Während die s’s die Schätzer für die \(\beta\)s sind, ist das \(e_i\) kein Schätzer für \(U_i\). Das liegt daran, dass das \(e_i\) nur eine Fehlerstreuung in der Stichprobe ist und \(U_i\) viel mehr angibt, dass unberücksichtigte Einflussgrössen und ein stochastischer Rest nicht vom Modell abgebildet sind.
\[ Y_i = b_1 + b_2X_{i2} + b_3X_{i3}+e_i \tag{2.2}\]
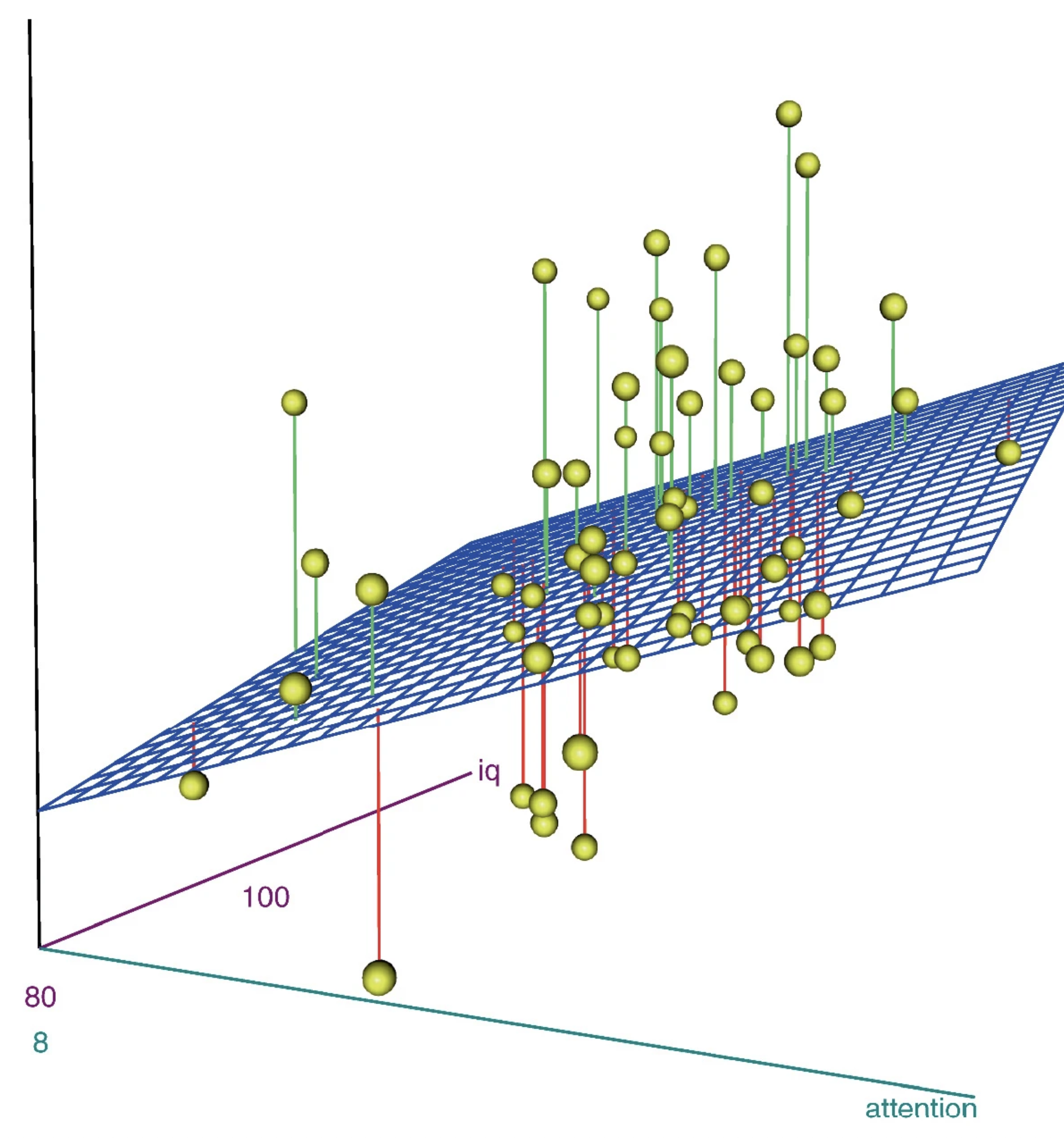
Bei einer Regression mit zwei UVs wird praktisch eine Ebene in die Punktwolke gelegt (siehe Abbildung 2.3). Wir schätzen aber eine multivariate Regression, damit wir bivariat interpretieren können, also je UV sagen, wie stark der Effekt auf die AV ist. Insofern interpretieren wir je Variable nur ein b, was dem Ansteig (Zusammenhang) einer UV mit der AV entspricht. Das können wir machen, weil die Statistik beziehungsweise unser Statistikprogramm die «Kontrolle» der übrigen Variablen übernimmt und wir schön die kontrollierte bivariate Beziehung interpretieren können. Die b’s beschreiben dabei die Gerade, die die Ebene an der Stelle bildet, die für die andere Variable der Durchschnitt ist. Bei drei UVs spannen die b’s zusammen eigentlich einen Raum auf, was sich aber niemand mehr visuell vorstellen kann. Die Statistik kann das aber und erledigt das so für uns, dass wir uns immer nur die Beziehungen anhand der jeweiligen b’s der einzelnen UV’s anschauen können.
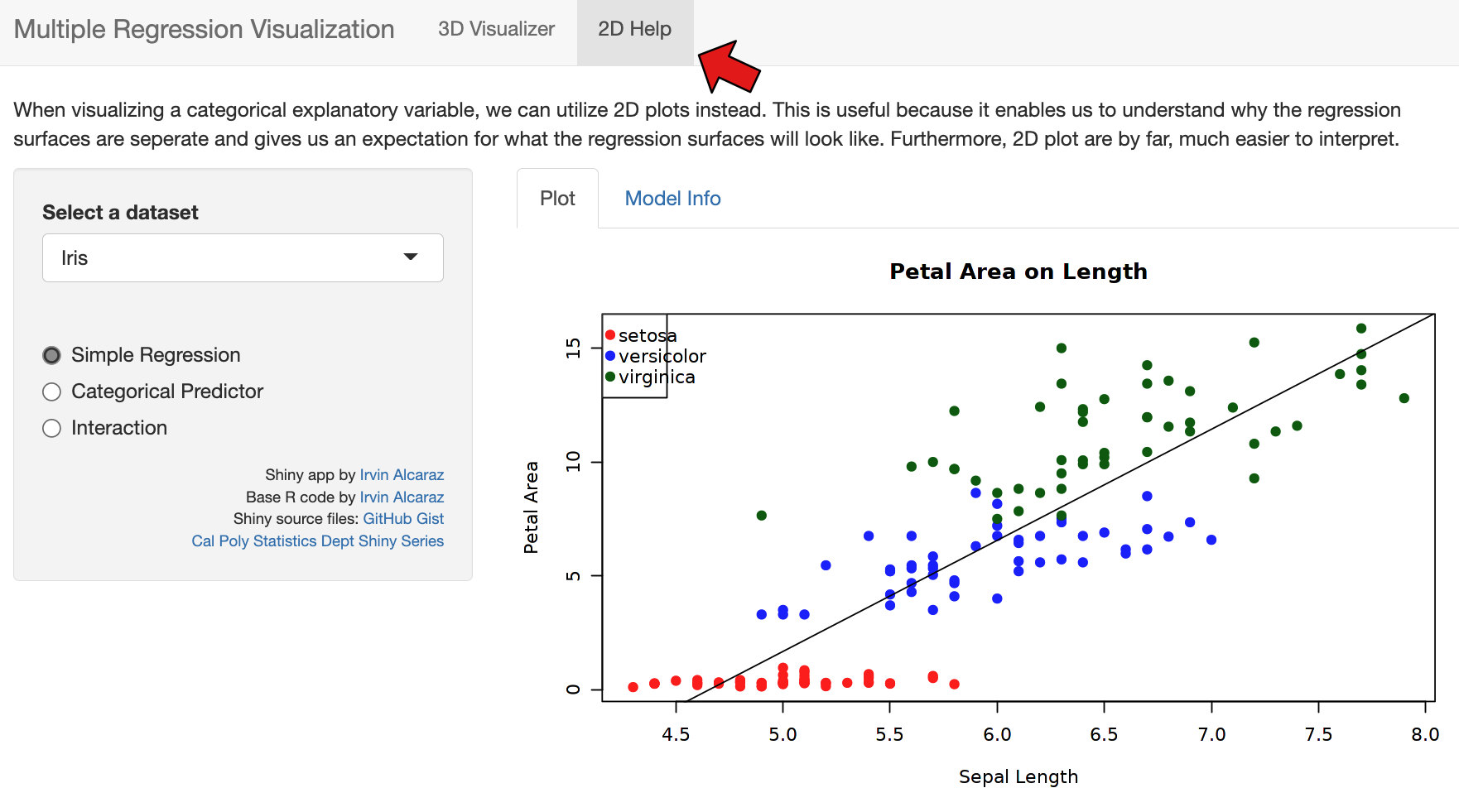
Hier wird eine Regression recht gut als Punktwolke visualisiert: http://shiny.calpoly.sh/3d_regression/.
Zwischenaufgabe: Schreiben Sie die Formel für die einfache bivariate Regression auf?
\[ Y_i = b_1 + b_2X_{i2} + e_i \]
2.4 Die Regressionskoeffizienten b
2.4.1 Im bivariaten Modell
Das b ist im bivariaten Modell: \(b = \frac{\sum{(X- \overline{X})(Y- \overline{Y})}}{\sum{(X- \overline{X})^2}}\). Wenn Sie genau hinsehen, erkennen Sie über dem Bruch den oberen Teil der Kovarianz \(\sum{(X- \overline{X})(Y- \overline{Y})}\) und im unteren Teil der Varianz von X (ohne dass jeweils durch n geteilt wird). Nachem man das ein bisschen umgestellt hat, erhält man \(r_{YX}\cdot \frac{s_y}{s_X}\) und wenn man durch \(\frac{s_y}{s_X}\) geteilt hat, steht da, dass \(r_{YX} = b \cdot \frac{s_X}{s_Y}\) ist. Im Grunde ist die Korrelation also ein standardisiertes b.
2.4.2 Bei zwei UVs und zwei b’s
Wenn wir mit Hilfe der Ordenary-Least-Squares-Methode (OLS) eine Formel für die b’s bestimmt haben, kommt folgende Formel Gleichung 2.3 für das \(b_2\) der Variable \(X_2\)1 heraus:
\[ \begin{aligned} b_2 & = \frac{r_{y2}-r_{23}r_{y3}}{(1-R_{2.3}^2)}\frac{s_y}{s_2} \end{aligned} \tag{2.3}\]
Die Formel hat es in sich. Aber schauen Sie sich die Formel mal ganz in Ruhe und stückchenweise an. Als eines der ersten Elemente taucht \(r_{Y2}\) auf, was so viel heisst, wie die einfache Korrelation zwischen Y und der ersten X-Variable (also \(x_2\)), die ja das \(b_2\) hat und darum kurz und knapp nur noch mit dem Subscript 2 bedacht wird. Also hängt das b mit der Korrelation zwischen der zugehörigen X-Variable und Y zusammen. Da b skalenabhängig ist und r nicht, steht hinten noch dieses \(\frac{S_Y}{S_2}\), also die Standardabweichung von \(Y\) geteilt durch die Standardabweichung von \(X_2\). Dieser Bruch sorgt nur dafür, dass b in der Skala von Y angegeben ist (darum auch multipliziert mit \(s_Y\)) – den Teil können Sie schon mal vergessen.
Interessanter ist der zweite Teil der Gleichung über dem Bruchstrich: Wir ziehen da das Produkt aus \(r_{23}\) und \(r_{Y3}\) ab. Das heisst, wir gehen von der bivariaten Korrelation aus, rechnen jetzt aber noch die Korrelation raus, die die beiden unabhängigen Variablen \(X_2\) und \(X_3\) untereinander haben. Wir ziehen allerdings nicht einfach \(r_{23}\) ab, sondern multiplizieren das auch noch mit \(r_{Y3}\). Das bedeutet, wir haben einen Zusammenhang \(r_{y2}\) und rechnen aus dem den Anteil gemeinsamer Varianz, also der Zusammenhänge der Varialbe \(x_2\) heraus (wir subtrahieren sie), die diese mit \(X_3\), wobei wir nur so viel rausrechnen, wie die dritte Variable \(X_3\) wiederum mit Y gemeinsam hat. Wären die beiden Variablen \(X_2\) und \(X_3\) unkorrelliert, dann wäre auch das Produkt \(r_{23}r_{Y3} = 0\), weil \(0 \cdot r_{Y3} = 0\). Wenn \(X_2\) und \(X_3\) korrellieren, aber \(X_3\) und Y nicht, dann würden wir auch nichts von \(r_{Y2}\) abziehen. Im Storchenbeispiel würden wir also sagen, wir sehen den Zusammenhang zwischen Geburtenrate und Anzahl Störche. Wir müssen aber von dieser Korrelation abziehen, dass die Drittvariable \(X_3\) «Bevölkerungsdichte» (Stadt vs. Land) stark mit der zu erklärenden Geburtenrate \(Y\) korrelliert und diese mit der Anzahl der Störche (\(X_2\)), die in einer Region leben. Wie wir wissen, ist diesem Fall \(r_{23}r_{Y3} \approx r_{Y2}\) und darum der kausale Zusammenhang zwischen Storchenpopulation und Geburtenrate nicht gegeben.
2.4.3 Der standardisierte Regressionskoeffizient
Der standardisierte Regressionskoeffizient BETA (nicht \(\beta\)) entspricht im Fall der bivariaten Regression der Korrelation \(r_{YX}\).
2.4.4 Signifikanz der b’s und BETAs
Die b’s und BETAs können daraufhin geprüft werden, ob sie signifikant von 0 verschieden sind. Dafür wird ein t-Test gemacht, wie er auch bei Mittelwertvergleichen oder der Korrelation verwendet wird. Der t-Test spuckt dann einen p-Wert aus und wenn der kleiner ist als .05, dann sagen wir, dass ein b (oder auch sein BETA) signifikant von 0 verschieden sind. Das bedeutet, dass die Wahrscheinlichkeit kleiner als 5 Prozent (0.05) ist, dass das b rein zufällig so gross ist, wie es eben ist. Die Frage lautet also: Bei so einem gegebenem b, können wir da mit hoher Wahrscheinlichkeit ausschliessen, dass das währe \(\beta\) in Wirklichkeit 0 ist oder sogar das entgegengesetzte Vorzeichen hat (bei positivem b also kleiner ist als 0)?
2.5 Das Bestimttheitsmass \(R^2\)
Das Bestimmtheitsmass gibt an, wie gut die Werte der AV durch die Werte der UV vorhergesagt werden können. Im
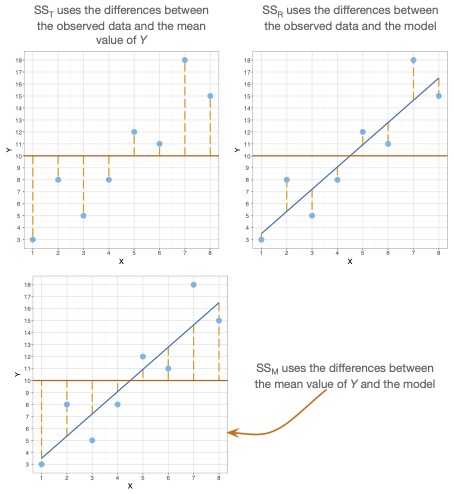
Wie viel von der Varianz der AV durch ein Modell aufgeklärt werden kann, stellt man fest, indem zunächst die Summe der quadrierten Abweichungen (Sum of Squares) für alle \(Y_i\) Werte gezählt werden. Also die totale Varianz der AV, die geschrieben wird als \(SS_T\) (Sum of Squares Total). Jetzt ist die Frage, wie viel von dieser Sum of Squares Total durch die Sum of Squares des Modells (\(SS_M\)) erklärt werden kann. Darum setzen wir diese beiden Summen der Quadrate (wenn man jeweils durch n teilen würde, wären das die Varianzen) ins Verhältnis zueinander und bekommen einen Prozentwert. Also rechnen wir \(\frac{SS_M}{SS_T}\) und bekommen einen Wert zwischen 0 und 1 bzw. 0% und 100% (% heisst ja «von Hundert» bzw. «geteilt durch 100»). Das ist der aufgeklärte Varianzanteil und den nennen wir \(R^2\).
- \(SS_T\): Summe der quadrierten Abweichungen für die AV (Y).
- \(SS_M\): Summe der quadrierten Abweichungen des Modells (der Punkte auf der Geraden, bzw. die geschätzten \(\hat{Y_i}\)-Werte).
Also: \(R^2 = \frac{SS_M}{SS_T}\)
Bei dieser Gleichung 2.4 können wir durch n teilen, also über und unter dem Bruch \(1/n\) ergänzen und hätten:
\[ \begin{aligned} R^2 & = \frac{SS_M/n}{SS_T/n} \end{aligned} \tag{2.4}\]
Was in Worten ausgedrückt bedeutet:
\[ \begin{aligned} R^2 & = \frac{\text{aufgeklärte Varianz}}{\text{Gesamtvarianz}} \end{aligned} \tag{2.5}\]
In der Abbildung 2.4 ist im ersten Quadrat die Abweichung der gemessenen Werte vom Mittelwert von Y dargestellt. Das ist die Summe der quadrierten (Sum of Squares \(SS_T\)) insgesamt (total) der AV, also Y. Würde man, wie oben, durch n teilen, wäre das einfach die univariate Varianz von Y. Wo X dabei liegt, ist völlig unbedeutend, da die Schätzung von Y an jeder Stelle von X gleich ist, also die Gerade parallel zu der x-Achse verläuft. Im zweiten Quadrat sind die Abstände zwischen der Regressionsgeraden und den tatsächlichen Werten dargestellt. Diese Abstände geben die Fehler wieder, die wir auch Residuen nennen, weshalb ihre Quadratsumme mit \(SS_R\) gekennzeichnet wird. Im letzten Quadrat ist die Summe der Abstände zwischen dem 0-Modell (orange Linie parallel zur X-Achse) und den geschätzten Werten, also denen, die auf der Modell- beziehungsweise Regressionsgeraden liegen. Deren Quadratsumme wird als \(SS_M\) gekennzeichnet.
Mit dem Bestimmtheitsmass können wir angeben, wie gut ein Modell insgesamt ist. Wir werden später noch diskutieren, wie sinnvoll das ist.
2.5.1 Das korrigierte \(R^2\)
Wenn man in ein Regressionsmodell mehr und mehr UVs aufnimmt, dann kann sich \(R^2\) nur vergrössern, weil die jeweils bestehende Aufklärung der AV nicht verkleinert, wenn man noch fragt, was eine weitere Variable für die Aufklärung der AV leisten kann. Im Gegenteil: Es wird selbst dann ein bisschen von der AV erklärt, wenn es garkeinen Zusammenhang zwischen einer UV und der AV gibt. Es gibt also zufällige «Varianzaufklärung» (die in 95% der Fälle nicht signifikant ist und uns daher eigentlich egal sein könnte). Wenn man aber etliche UVs ins Modell aufnimmt, die alle keinen Zusammenhang mit der AV haben, kann es sein, dass \(R^2\) irreführend gross wird. Darum korrigiert man bei kleinen Stichproben das \(R^2\) ein bisschen um die Anzahl der UVs (die Anzahl der UVs wird mit «k» gekennzeichnet.).
Wenn unser Stichprobenumfang n klein ist und k ähnlich gross, dann ist \(n-k-1\) deutlich kleiner als \(n-1\) und damit der Korrekturfaktor \(\frac{n-k-1}{n-1}\) klein, was zu einer starken Korrektur von \(R^2\) führt.
2.5.2 Der F-Test zum \(R^2\)
LEF 2
Essayfragen 2
E2.1 Wie ist die Korrelation definiert?
E2.2 Was ist das Analyseziel einer Regression?
E2.3 Wie sind die Regressionskoeffizienten gekennzeichnet? (Welcher Buchstabe)
E2.4 Was ist der Unterschied zwischen BETA und \(\beta\)?
E2.5 Was drückt der Standardfehler der Regressionskoeffizienten b aus?
E2.6 Mit welchen Kennwerten kann die Modellgüte insgesamt bewertet werden?
E2.7 Was ist a) \(R^2_{adj.}\) und b) wann würde man es verwenden?
E2.8 Was sagt die Signifikanz des F-Tests für ein Regressionsmodell aus?
MC-Fragen 2
MC 2.1.
MC 2.2.
MC 2.3.
MC 2.4.
MC 2.5.
MC 2.6.
Für LEF 2: von Punkten, was % und etwa einer entspricht.
In den tiefergestellten Subscripten steht bei den r’s immer nur 2. Das heisst \(r_{Y2}\) kennzeichnet die Korrelation zwischen \(Y\) und \(X_2\).↩︎